
练习设a>b>c>0,x,=a"+b"+c",求limxn>00a<x,<a.3解 由于以及lima./3= lima.3n =a.1lima = a,n→00n→n-0夹逼定理limx, = a.1n-→00练习:lim(2n)n-8福
解 由于 以及 lim , n a a 夹逼定理 lim . n n x a a 1 lim 3 1 n n a a 3 n a lim 3 n n a 0, , lim n n n n n n n a b c x a b c x 练习 设 求 n x 2 2 2 1 1 1 lim 1 2 n n n n 练习:

证明lim/n =1练习n→8证:当n>1时n>l,记a,=n=1+h,则有n(n-1)n(n-1)h2h2 ≥n=(1+h,)"≥1+nh,+22220≤h或0≤h,≤<nn-1n-122于是1≤a,=1+h,≤1+而 lim1+1二n-1n→所以limn =1n0
lim 1 n n n 练习 证明 1 1 1 n n 证:当n n a n h 时, ,记 n n,则有 2 2 2 ( -1) ( -1) (1 ) 1 2 2 2 2 0 0 1 1 n n n n n n n n n n n n h nh h h h h n n , 或 2 2 1 1 1 lim1 1 1 1 lim 1 n n n n n a h n n n 于是 ,而 , 所以

sinx(1)limx→0xX7AD元设单位圆 O,圆心角ZAOB= x,(0<x<一2作单位圆的切线,得△ACO.扇形OAB的圆心角为x,△OAB的高为BD,于是有sinx=BD, x=AB,tanx = AC
(1) 0 sin lim 1 x x x , , (0 ) 2 . , , sin , , tan , O AOB x x ACO OAB x OAB BD x BD x AB x AC 设单位圆 圆心角 作单位圆的切线,得 扇形 的圆心角为 的高为 于是有 A C x o B D

sinx即cosx<<1,.. sinx < x < tanx.x"时,元上式对于_元<x<0也成立。当0<x<22xx-20<|cosx-1 =1-cosx = 2sin22(?29lim= 0, :. lim(1 - cos x) = 0,2x-→0x-0sinx limcosx = 1, 又::lim1=1,=1...limx-→0x-0x-0X
sin x x tan x, 1, sin cos x x 即 x 0 . 2 x 上式对于 也成立 , 2 当 0 时 x 0 cos x 1 1 cos x 2 2sin2 x 2 ) 2 2( x , 2 2 x 2 0 lim 0, x 2 x lim(1 cos ) 0, 0 x x limcos 1, 0 x x 0 lim1 1, x 又 0 sin lim 1. x x x
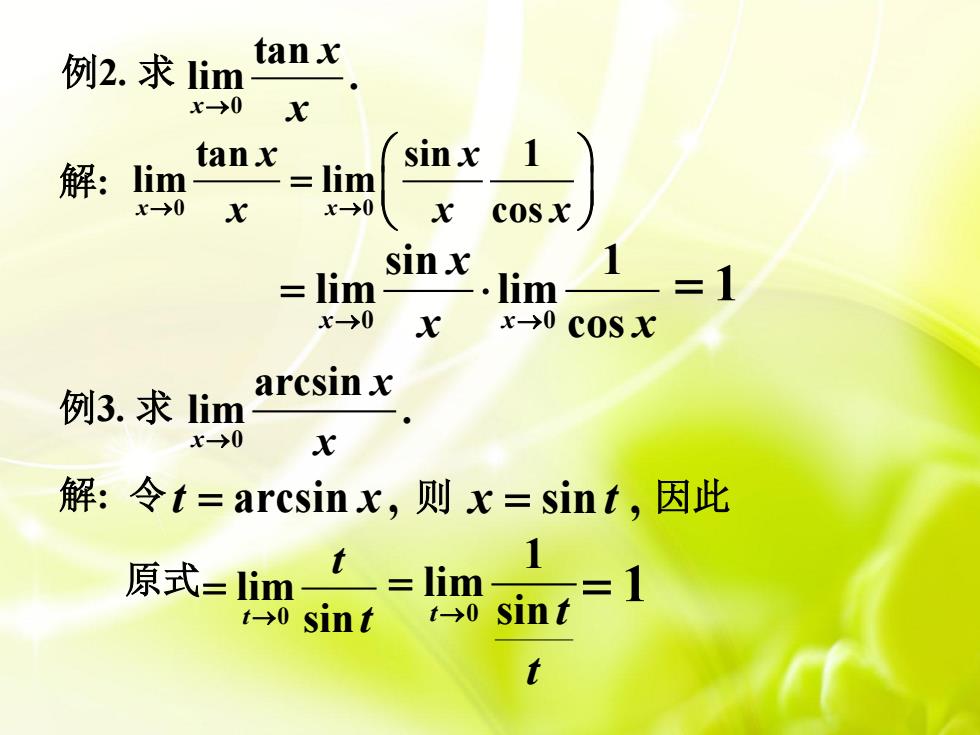
tanx例2. 求 limx-→0tanxsin x解: limlim-x-→0x-0xxcosx1sinx=1lim= limx-0x-0xcosxarcsin x例3. 求 limx-0x解:令t=arcsinx,则 x=sint,因此1t原式=limJimsintt-→0t-→0sintt
例2. 求 0 tan lim . x x x 解: 0 0 tan sin 1 lim lim x x cos x x x x x 0 0 sin 1 lim lim x x cos x x x 1 例3. 求 0 arcsin lim . x x x 解: 令 t x arcsin , 则 x t sin , 因此 原式 0 lim t sin t t 0 1 lim t sin t t 1