
证明 S'rdss'rods (a<b) 证明:显然-fx≤f(x)≤f(x 由推论1 ∫/xs∫fxwd≤∫fx 0 f()ds∫af(xl k (a<b)
证明 () () b b a a f x dx ≤ f x dx ∫ ∫ (a b < ) 证明: 显然 − ≤≤ f () () () x f x f x () () () b bb a aa − ≤≤ f x dx f x dx f x dx ∫ ∫∫ () () b b a a f x dx f x dx ≤ ∫ ∫ (a b < ) 由推论 1

五、定积分的性质 性质6:设M,m分别是函数f(x) 性质7(积分中值定理) 在[a,1上的最大值和最小值, 若fx)在[a,b连续 则 则在[a,b1内至少存在一点5,使 mb-a)s∫fx)ds≤M(b-a) ∫fx)dk=f传b-a) 估计积分值的大 致范围 积分中值公式
五、定积分的性质 性质 6:设M ,m分别是函数 f ( ) x 在[,] a b 上的最大值和最小值, 则 ( ) () ( ) b a m b a f x dx M b a − ≤ ≤− ∫ 估计积分值的大 致范围 性质 7 (积分中值定理) 若 f ( ) x 在[,] a b 连续 则在[,] a b 内至少存在一点ξ ,使 ( ) ( )( ) b a f x dx = f ξ b a − ∫ 积分中值公式
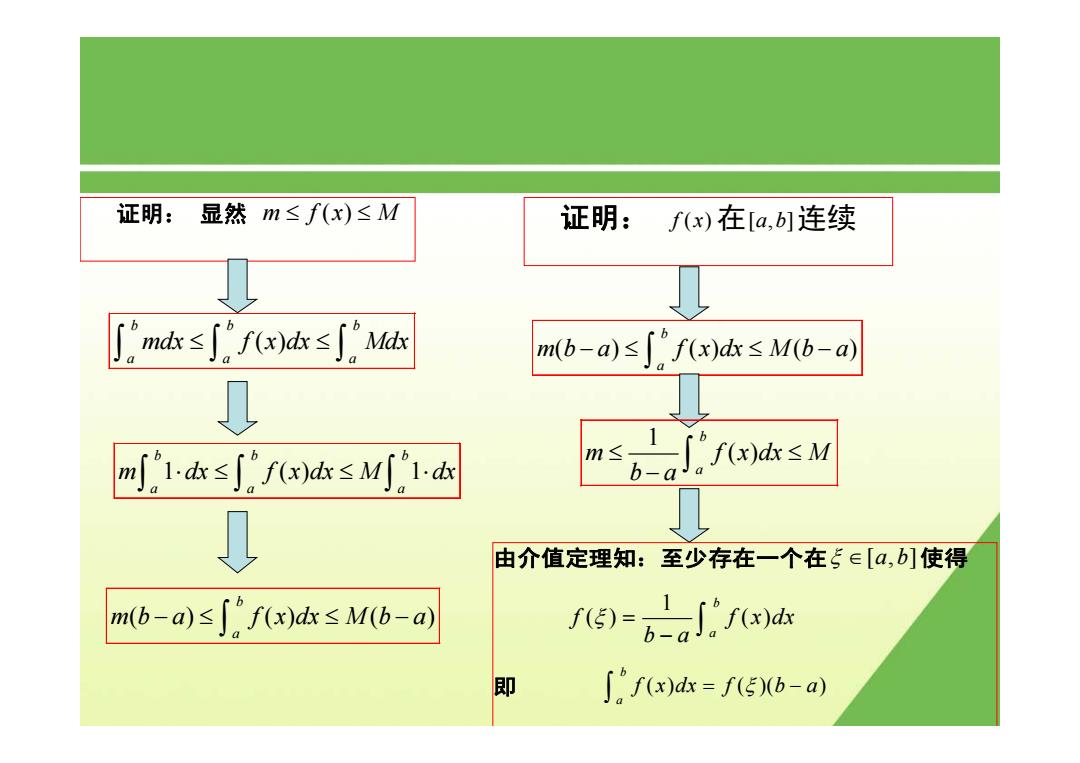
证明:显然m≤f(x)≤M 证明:f(x)在[a,b1连续 [mk≤∫fe)本≤∫M m(b-a)≤∫fx)dk≤Mb-a)) m21≤∫f()ds≤M1s sa」 由介值定理知:至少存在一个在5∈[a,b]使得 m(b-a))sjfx)ak≤Mb-a f5-。aes 即 ∫f(x)=f5b-a)
证明: 显然 m fx M ≤ ≤ ( ) ( ) bb b aa a mdx ≤ ≤ f x dx Mdx ∫∫ ∫ 1 () 1 bb b aa a m dx ⋅ ≤ ≤⋅ f x dx M dx ∫∫ ∫ ( ) () ( ) b a mb a −≤ ≤ − f x dx M b a ∫ 证明: f ( ) x 在[,] a b 连续 ( ) () ( ) b a m b a f x dx M b a − ≤ ≤− ∫ 1 ( ) b a m f x dx M b a ≤ ≤ − ∫ 由介值定理知:至少存在一个在ξ ∈[,] a b 使得 1 () () b a f f x dx b a ξ = − ∫ 即 ( ) ( )( ) b a f x dx = f ξ b a − ∫
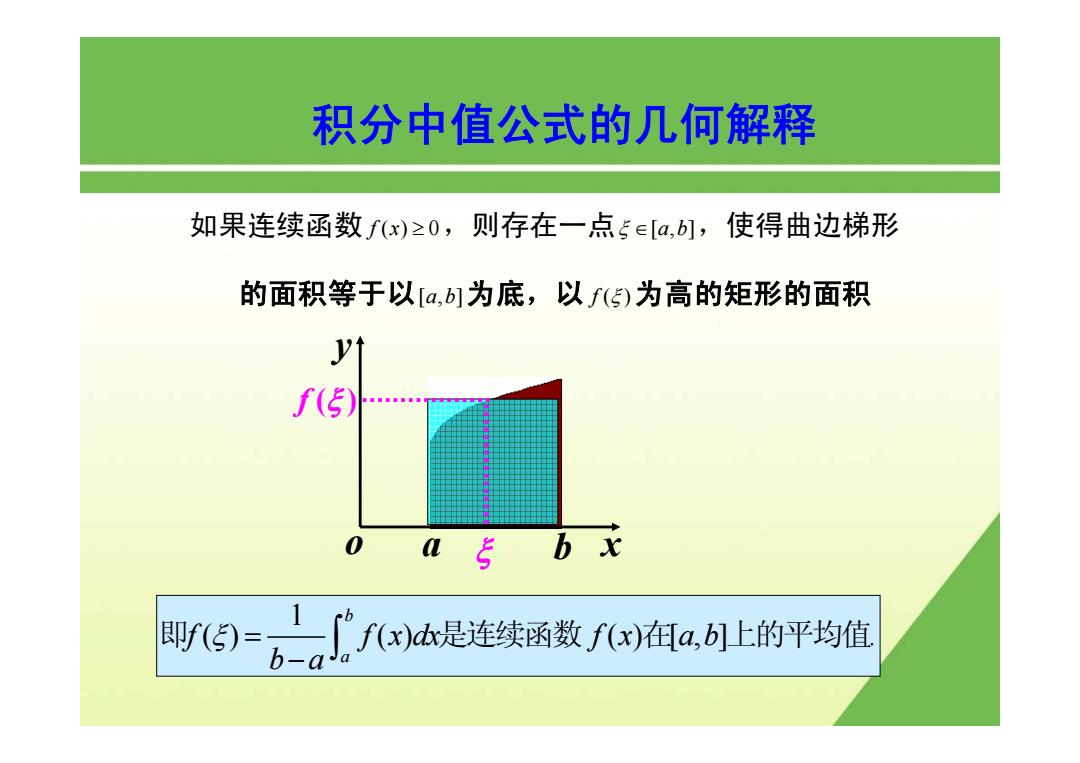
积分中值公式的几何解释 如果连续函数fx)≥0,则存在一点5∈[a,b1,使得曲边梯形 的面积等于以[a,b]为底,以f()为高的矩形的面积 f(5) 0 05 听G=6a广fh是连续函数fa,上的平均值
积分中值公式的几何解释 x y o a ξ b f (ξ ) 1 () () () [,] . b a f f x dx f x a b b a ξ = − 即 是连续函数 在 上的平均值 ∫ 如果连续函数 f x() 0 ≥ ,则存在一点 ξ ∈[,] a b ,使得曲边梯形 的面积等于以[,] a b 为底,以 f ( ) ξ 为高的矩形的面积

五、定积分的性质 例2判断正误, ④rdk≤r 2)6≤(x2+≤51
例 2 判断正误. 五、定积分的性质 1 1 2 3 0 0 (1) . x dx x dx ≤ ∫ ∫ ( ) 4 2 1 (2) 6 1 51 ≤ +≤ x dx ∫