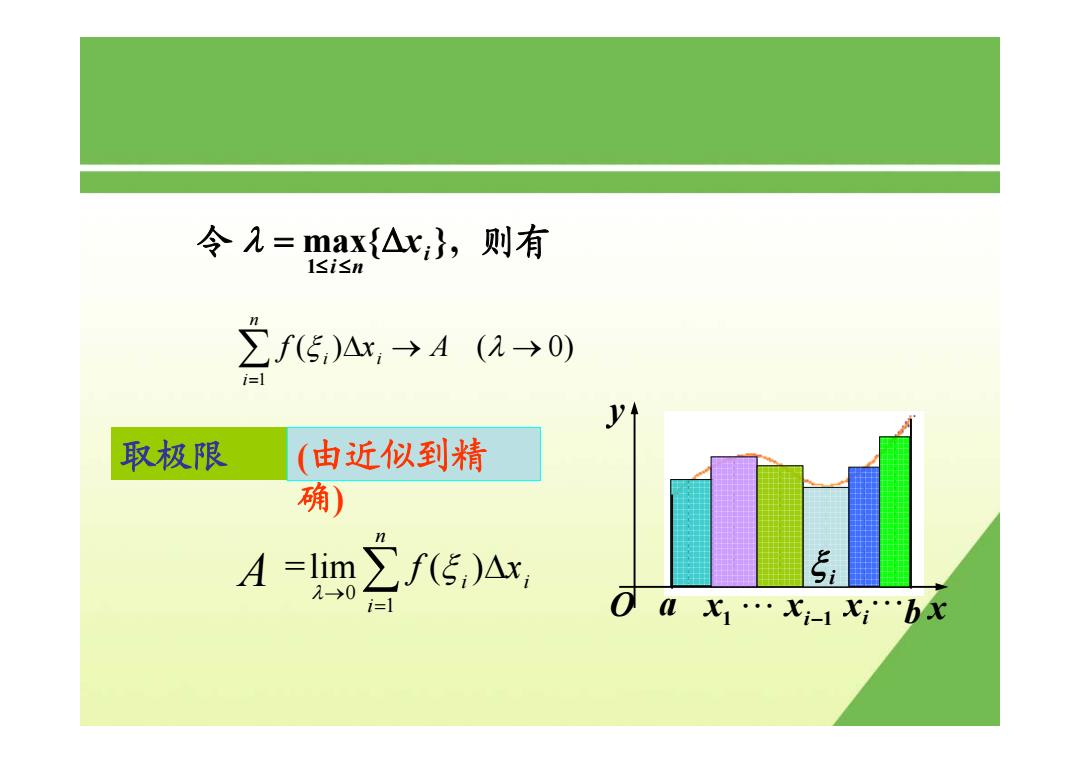
令九=max{△x},则有 l≤i≤n 2fE,Ax,→4(U→0) i= 取极限 (由近似到精 确) A=lim∑f(5,)Ax 5 -→01 O0飞1…X;-1x:…bx
取极限 令 max{ }, 1 i i n = Δx ≤ ≤ λ 则有 0 1 = lim ( ) n i i i f x λ ξ → = ∑ Δ a b x y O 1 x xi−1 xi ξ i " " (由近似到精 确) A 1 ( ) ( 0) n i i i f xA ξ λ = ∑ Δ→ →

二、定积分的定义 设函数f(x)在[a,b]上有界 在[a,b]中任意插入若干个分点 a=x0<X1<…<X-1<x,<…<xm-1<xn=b 将区间[a,b1划分为n个小区间[x-,x]各个小区间的长度依次为△x,=x,-x- 在每个小区间[x-,x]上任取一点5,作乘积f5)△x(i=1,2,…,n),并求和 S,=∑f(5)△x i=l 记=max{Ax,} l≤≤n 如果不论对区间[a,b]怎样划分,也不论5∈[x-,x]怎样选取,只要2→0时, imS,=lm∑f⑤)Ay总存在都为1 10 10 则称I为fx)在[a,b]上的定积分,记为∫fxk=1=lim∑f(5)△x 20
设函数 f ( ) x 在[,] a b 上有界 二、定积分的定义 在[,] a b 中任意插入若干个分点 01 1 1 ii nn ax x x x x x b = <<< <<< < = " " − − 将区间[,] a b 划分为n 个小区间 1 [ ,] i i x x − 各个小区间的长度依次为 i ii 1 x x x Δ = − − 在每个小区间 1 [ ,] i i x x − 上任取一点 i ξ ,作乘积 ( )i i f ξ Δx (i n =1, 2, , " ),并求和 1 ( ) n n ii i S fx ξ = = ∑ Δ 记 1 max{ }i i n λ x ≤ ≤ = Δ 如果不论对区间[,] a b 怎样划分,也不论 1 [ ,] i ii ξ x x ∈ − 怎样选取,只要λ → 0时, 0 0 1 lim lim ( ) n n ii i S fx λ λ ξ → → = = ∑ Δ 总存在都为I 则称I 为 f ( ) x 在[,] a b 上的定积分,记为 0 1 ( ) lim ( ) n b i i a f x dx I f x λ ξ → ∫ == Δ ∑

积分上限 积分和 f(x)卡J=0 lim∑f(5,)△x, i= 积分下限 被积函数 [a,b]积分区间 被积表达式 积分变量 求总量的数学模型,在不同 的领域有不同的应用
∫ = = ba f ( x)dx I 1 0 l mi ( ) n i i i f x λ ξ = → ∑ Δ 被积函数 被积表达式 积分变量 [a,b]积分区间 积分上限 积分下限 积分和 求总量的数学模型,在不同 的领域有不同的应用

比较 定积分 不定积分 (1)定积分∫fx)k是-个数量 (1)不定积分∫f(x)是f(x)的所有原函数 2) 定积分∫fx只与被积函数f(,)及(2)不定积分∫f(x):只与被积函数f(x 积分区间[a,b]有关,与积分变量记号无关 和积分变量记号有关. 即j。f(x=∫2fu=fud 即:若∫f(x)d=F(x)+C,则 ∫fw)du=F(u)+C
比 较 定积分 不定积分 (1) 定积分 () b a f x dx ∫ 是一个数量. (1)不定积分 f ( ) x dx ∫ 是 f ( ) x 的所有原函数 (2) 定积分 () b a f x dx ∫ 只与被积函数 f ( ) x 及 积分区间[,] a b 有关,与积分变量记号无关 即 ( ) b a f x dx ∫ ( ) () b b a a = = f u du f t dt ∫ ∫ (2) 不定积分 f ( ) x dx ∫ 只与被积函数 f (x) 和积分变量记号有关. 即: 若 f () () x dx F x C = + ∫ ,则 f () () u du F u C = + ∫
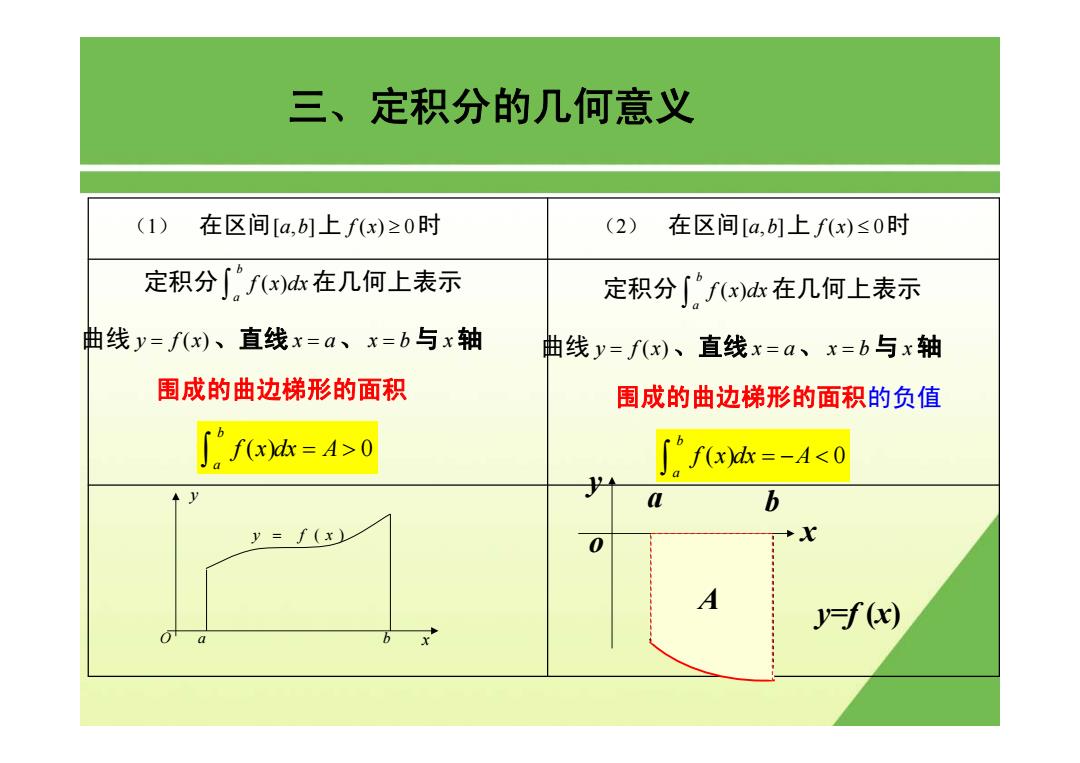
三、定积分的几何意义 (1)在区间[a,b1上f(x)≥0时 (2) 在区间[a,1上f(x)≤0时 定积分∫。f(x)d在几何上表示 定积分∫fx)d在几何上表示 曲线y=f(x)、直线x=a、x=b与x轴 曲线y=f(x)、直线x=a、x=b与x轴 围成的曲边梯形的面积 围成的曲边梯形的面积的负值 f=A>0 ∫2f达=-4<0 a b y f(x) A y=f(x)
(1) 在区间[,] a b 上 f x() 0 ≥ 时 三、定积分的几何意义 定积分 ( ) b a f x dx ∫ 在几何上表示 曲线 y fx = ( )、直线 x a = 、 x b = 与 x轴 围成的曲边梯形的面积 () 0 b a f x dx A = > ∫ x y O a b y = f ( x ) (2) 在区间[,] a b 上 f x() 0 ≤ 时 定积分 ( ) b a f x dx ∫ 在几何上表示 曲线 y fx = ( )、直线 x a = 、 x b = 与 x轴 围成的曲边梯形的面积的负值 () 0 b a f x dx A = − < ∫ o x y a b y=f (x) A