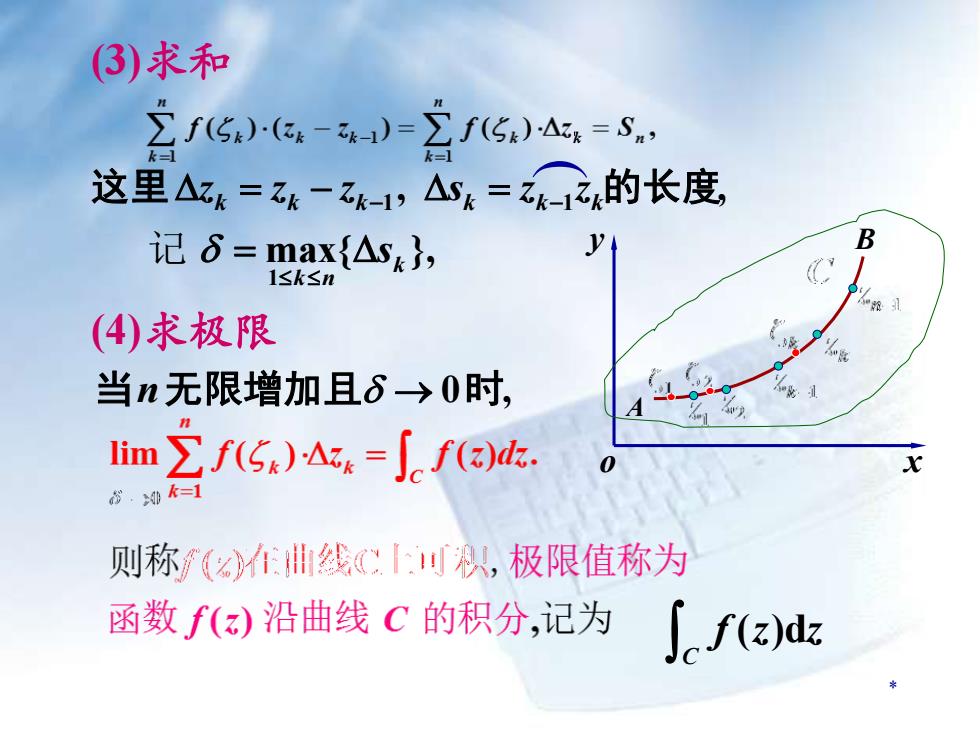
(3)求和Ef(5t)(2k - zh-1)-Ef(5r)Az = Sn,这里Az = Zk-Zk-1, Ask= zk-1z,的长度,By记8=max(As,1≤k≤n(4)求极限e当n无限增加且s→0时hee-limE f(5)△=f, f(z)dzx0=1则称(在曲线叫,极限值称为函数f(z)沿曲线 C 的积分,记为Jc f(z)dz
* o x y A B 1 记 max{ }, k k n s = , , 这里zk = zk − zk−1 sk = zk−1 zk的长度 当n无限增加且 → 0时, (3)求和 (4)求极限 ( )d C f z z

注意:1:对C的分法无关2:与5k的取法无关说明:(1) 用[-f(z)dz表示f(z)沿着曲线C的负向的积分(2)f(z)沿着此闭曲线C的积分也可记为Φf(z)dzC
* 说明 : (2) ( ) ( )d . C f z C f z z 沿着此闭曲线 的积分也可记为 (1) ( )d ( ) C f z z f z 用 − 表 示 沿 着 曲 线C 的 负 向 的 积 分 1: 对 的 分 法 无 关 2: 与 k 的 取 法 无 关 C 注意:

2.积分存在的条件及积分性质如果f(z)是连续函数而C是光滑曲线时积分Jf(z)dz 一定存在Z.f(5.)AzkZ[u(5k, nk)+ iv(5k, ne)(Axe +iAyk)=k=lk=lE[u(5k, nk)Axs -v(5k, nk)Ayk ]-niZ[v(Eh,nk)Axh + u(5k,nk)Ayh)-[c f(z)dz = [_udx -vdy+if,vdx + udy
* 2. 积分存在的条件及积分性质 1 1 [ ( , ) ( , ) ] [ ( , ) ( , ) ] n k k k k k k k n k k k k k k k u x v y i v x u y = = = − + + − C udx vdy + C = + i vdx udy 1 ( ) n k k k f z = 1 [ ( , ) ( , )]( ) n k k k k k k k u iv x i y = = + + C f (z)dz 如果f(z)是连续函数而C是光滑曲线时, 积分 一定存在 C f (z)dz

公式 Jf(z)dz =[,udx - vdy+i,vdx + udy从形式上可以看成是f(z)=u+iv与dz=dx+idy相乘后求积分得到:J. f(z)dz = J (u + iv)(dx + idy)= J,udx + ivdx + iudy - vdy_udx - vdy + il vdx + udy
* f (z) = u + iv 与dz = dx + idy 相乘后求积分得到: C f (z)dz = + + C (u iv)(dx idy) = + + − C udx ivdx iudy vdy d d d d . = − + + C C u x v y i v x u y C f (z)dz − C udx vdy + C = + i vdx udy 从形式上可以看成是 公式

作业:如果f(z)沿曲线C是可积的,则f在C上有界可以使用反证法,亦即,若f在C上无界则必定在某一个分割[zk-1,zk]上|f(z)|无界
* 作业:如果f(z)沿曲线C是可积的,则f 在C上有界。 可以使用反证法,亦即,若f在C上无界, 则必定在某一个分割 上|f(z)| 无界