《概率论与数理统计》课程教学课件（PPT讲稿）第04章 随机变量的数字特征 4.1 数学期望

概率论与散理统外「 引例2射击问题 设某射击手在同样的条 件下，瞄准靶子相继射击90次， (命中的环数是一个随机变量) 射中次数记录如下 命中环数k 0 1 2 3 4 5 命中次数n 2 13 1510 20 30 频率 2 131510 2030 n 90 90 9090 90 90 试问：该射手每次射击平均命中靶多少环？

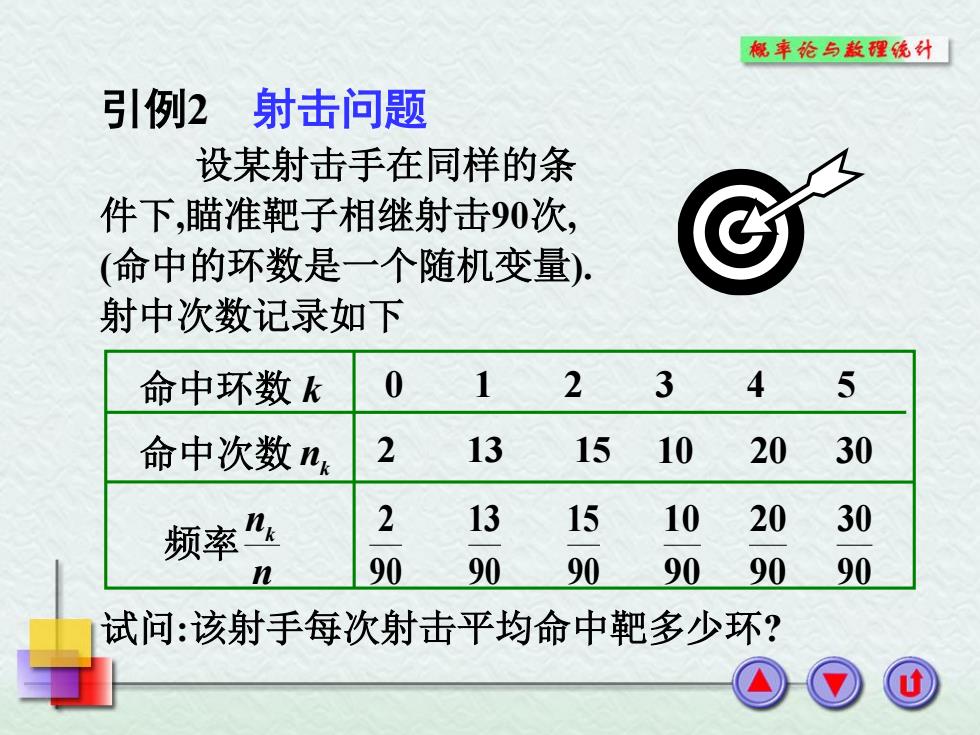
设某射击手在同样的条 件下,瞄准靶子相继射击90次, (命中的环数是一个随机变量). 射中次数记录如下 引例2 射击问题 试问:该射手每次射击平均命中靶多少环? 0 1 2 3 4 5 2 13 15 10 20 30 90 15 90 13 90 2 90 20 90 10 90 30 命中环数 k 命中次数 频率 nk n nk

概率论与散理统计 解平均射中环数= 射中靶的总环数 射击次数 0×2+1×13+2×15+3×10+4×20+5×30 90 2 13,15 =0× +1× +2×+3× 10 20 +4× 9090 90 90 90 30 +5x 90 =∑k k=3.37. n 设射手命中的环数为随机变量Y

解 平均射中环数 射击次数 射中靶的总环数  90 0 2  113  215  310  4 20  5 30  90 30 5 90 20 4 90 10 3 90 15 2 90 13 1 90 2 0               3.37.    5 k 0 k n n k 设射手命中的环数为随机变量 Y

概率论与散理统外「 平均射中环数 ∑k 41 一随机波动 频率随机波动 “平均射中环数”的稳定值=？ ∑k n-→o0 ∑kp: 随机波动 稳定值 “平均射中环数”等于 射中环数的可能值与其概率之积的累加

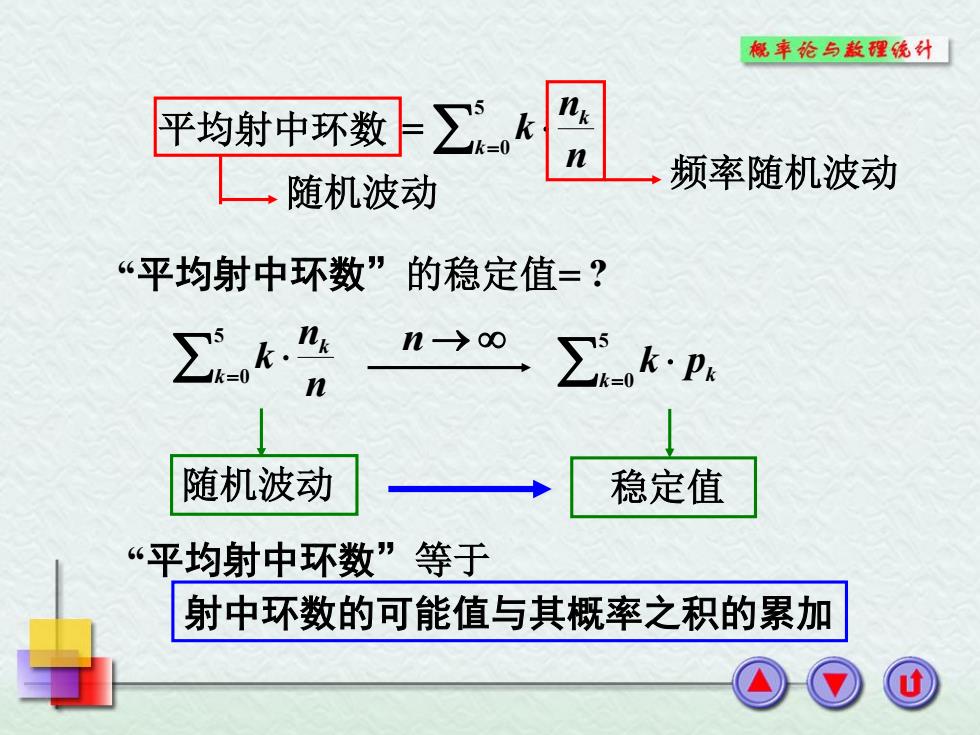
    5 k 0 k n n 平均射中环数 k 频率随机波动 随机波动    5 k 0 k n n k n      5 k 0 k pk 随机波动 稳定值 “平均射中环数”的稳定值  ? “平均射中环数”等于 射中环数的可能值与其概率之积的累加

概率论与敖理统计 1、离散型随机变量的数学期望 定义设离散型随机变量X的分布律为 P{X=Xx}=Pk,k=1,2,. 若级数∑xP:绝对收敛，则称级数∑1P k=1 的和为随机变量X的数学期望，记为E(X).即 E(X)=∑xP k-1

1、 离散型随机变量的数学期望 定义 1 1 1 { } , 1,2, . , , ( ). ( ) . k k k k k k k k k k k X P X x p k x p x p X E X E X x p              设离散型随机变量 的分布律为 若级数 绝对收敛 则称级数 的和为随机变量 的数学期望 记为 即

概率论与散理统外「 分赌本问题 A期望所得的赌金即为X的数学期望 3。 B(X0=200×+0×4150(元. 41 射击问题 “平均射中环数”应为随机变量Y的数学期 望 E(Y)= 0×P0+1×P1+2×P2+3×P3+4×P4+5×P5:

分赌本问题 A 期望所得的赌金即为 X 的数学期望 射击问题 “平均射中环数”应为随机变量Y 的数学期 望 0 1 2 3 4 5 . ( ) p0 p1 p2 p3 p4 p5 E Y             150( ). 4 1 0 4 3 E(X)  200    元