
©少本X上大军 由矩阵(3)可讨论方程组(1)的解的情况 1)若d,+1≠0,则方程组无解。 2)若d,+1=0,则方程组有解, 当 =n 有唯一解。 r<n 有无穷多解。 上页 这回
由矩阵(3)可讨论方程组(1)的解的情况 1) 若 dr+1 0 , 2) 若 1 0, r d + = 则方程组有解, 当 r n r n = 有唯一解。 有无穷多解。 则方程组无解

©山东理大军 主王二二王王王王王 定理4.1.1线性方程组(1)有解←→ R(A)=R(A) 证: 设 2 B L1 b A=(A,B)= L21 L24 am? 则方程组(1)与x01+x202+.+x,0Cn=B 等价 必要性 若方程组有解,则β可由x,2,.,an,线性表示 于是41,2,.,0n与0,a2,an,B等价. 即秩{a,2,an}=秩{a,2,.,anB} R(A)=R(A) 上页
定理4.1.1 线性方程组(1)有解 R(A) = R(A) 证: 设 ( , ) , 2 1 1 2 2 1 2 2 2 1 1 1 2 1 = = m m mn m n n b b b a a a a a a a a a A A 1 2 n 则方程组(1)与 1 1 2 2 n n x x x + + + = 等价. 必要性 若方程组有解,则 1 2 , , , , . 可由 n 线性表示 于是 1 2 1 2 , , , , , , , n n 与 等价. 即 R(A) = R(A) 秩 1 2 1 2 , , , , , , , n n = 秩

©少东理工大罩 充分性 若R(A)=R(A),即 秩{,a2,an}=秩{a,a2,an,B} 又因为 向量组01,02,.,Cn可由向量组01,02,0n,阝 线性表示, 因此向量组01,2,·,0n和向量组1,Q2,0nB有 王王 相同的最大无关组.因此B可由a,a2,an,线性表示 所以线性方程组(1)有解 推论1当R(4)≠R④时,方程组(1)无解. 推论2方程组(1)有唯一解←→R(A)=R(A) =n T推论3; 方程组(1)有无穷多解←→R(A)=R(A)<n 回
充分性 秩 1 2 1 2 , , , , , , , n n = 秩 若R(A) = R(A),即 1 2 , , , , . 因此 可由 n 线性表示 又因为 1 2 1 2 , , , , , , , 向量组 n n 可由向量组 线性表示, 1 2 1 2 , , , , , , , . 因此向量组 n n 和向量组 有 相同的最大无关组 所以线性方程组(1)有解. 推论1 当 R(A) R(A) 时,方程组(1)无解. 推论2 方程组(1)有唯一解 R A R A n ( ) ( ) = = 推论3 方程组(1)有无穷多解 R(A) = R(A) n
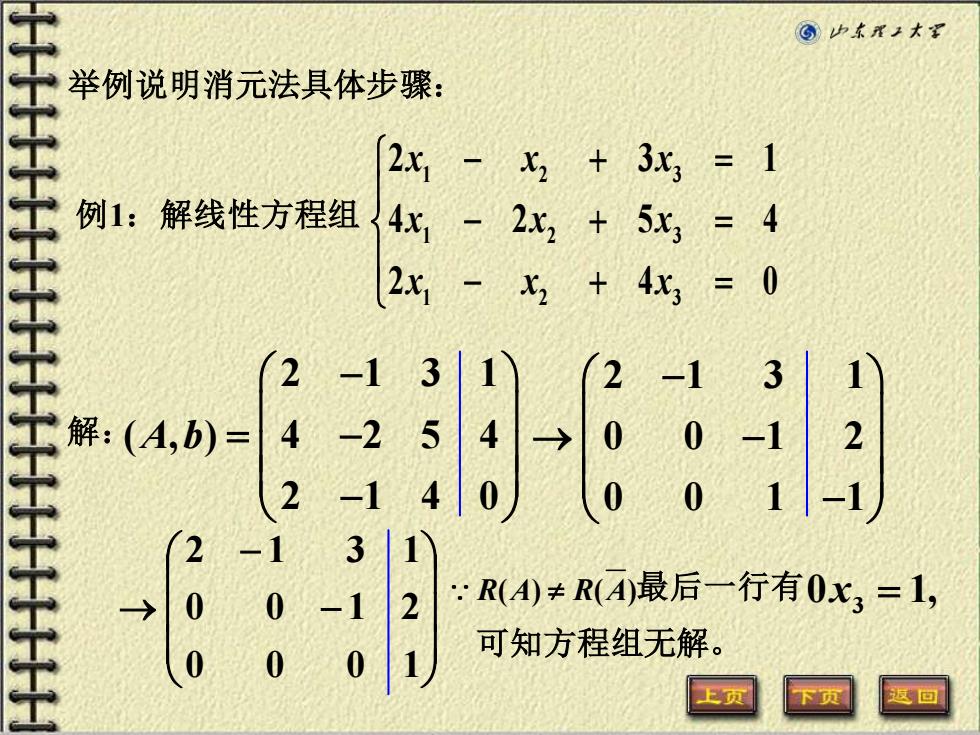
©)少东Y工大军 举例说明消元法具体步骤: 主主二二二主二二主主二二主二二王 2x X2 3x3 =1 例1:解线性方程组 4x 2x2 + 5x3 4 2x 4x3 =0 -1 3 一1 解: (A,b)= -2 2 -1 4 2 -1 3 0 0 -1 R(A)≠R(A)最后一行有0x3=1, 0 0 可知方程组无解 0
举例说明消元法具体步骤: 例1:解线性方程组 1 2 3 1 2 3 1 2 3 2 3 1 4 2 5 4 2 4 0 x x x x x x x x x − + = − + = − + = 解: − − → 0 0 0 1 0 0 1 2 2 1 3 1 2 1 3 1 0 0 1 2 0 0 1 1 − → − − 最后一行有 3 0 1, x = 可知方程组无解。 2 1 3 1 ( , ) 4 2 5 4 2 1 4 0 A b − = − − R A R A ( ) ( )