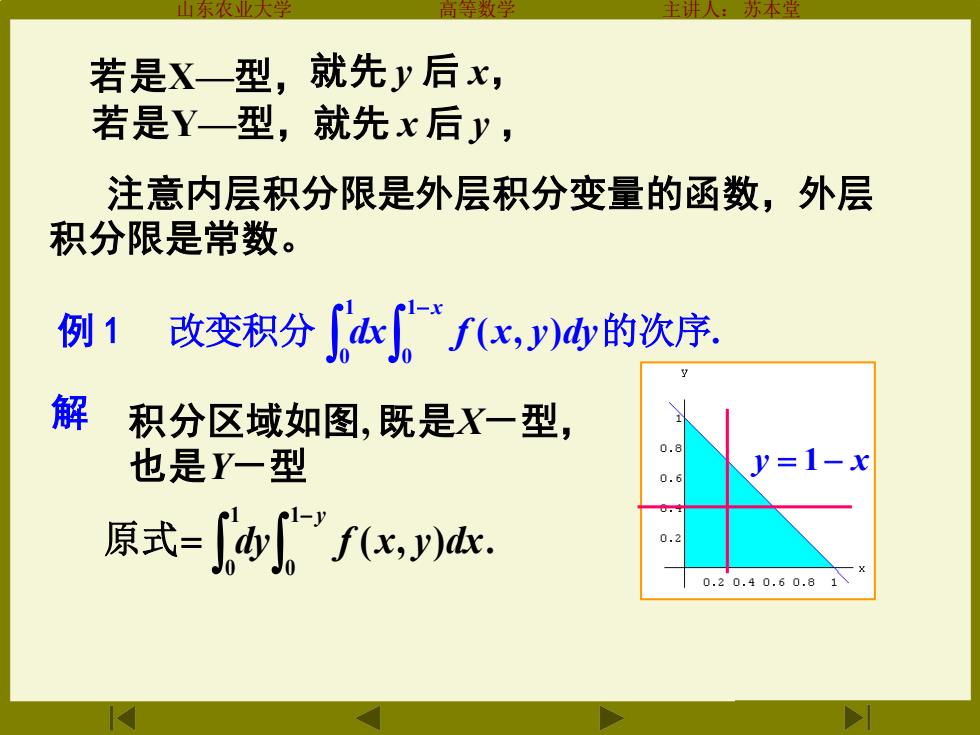
若是X一型,就先y后x, 若是Y一型,就先x后y, 注意内层积分限是外层积分变量的函数,外层 积分限是常数。 例1 改变积分”fc,y)的次序 解 积分区域如图,既是X一型, 也是Y一型 0.e y=1-x 0.6 原式=4fx,) 0.2 0.20.40.60.81
山东农业大学 高等数学 主讲人:苏本堂 若是X—型,就先 y 后 x, 若是Y—型,就先 x 后 y , 注意内层积分限是外层积分变量的函数,外层 积分限是常数。 例 1 改变积分 − x dx f x y dy 1 0 1 0 ( , ) 的次序. 解 积分区域如图, 既是X-型, 也是Y-型 y = 1− x 原式 − = y dy f x y dx 1 0 1 0 ( , )

本 例2改变积分 2f,p+dxf化,的次序 解积分区域如图 y=2-x 1.5 原式=pf
山东农业大学 高等数学 主讲人:苏本堂 y = 2 − x 2 y = 2x − x 例 2 改变积分 − − + x x x dx f x y dy dx f x y dy 2 0 2 1 2 0 1 0 ( , ) ( , ) 2 的次序. 原式 − − − = 1 0 2 1 1 2 ( , ) y y dy f x y dx. 解 积分区域如图

例3.交换下列积分顺序 1=x-22fx 解:积分域由两部分组成: J0≤y≤)x2 x2+y2=8 2≤x≤2W2 1 将D=D1+D2视为Y-型区域,则 22W2x 图- 1-.ys
山东农业大学 高等数学 主讲人:苏本堂 例3. 交换下列积分顺序 − = + 2 2 8 0 2 2 2 2 0 2 0 d ( , )d d ( , )d x x I x f x y y x f x y y 解: 积分域由两部分组成: , 0 2 0 : 2 2 1 1 x y x D 8 2 2 x + y = D2 2 2 y o 2 x D1 2 2 1 y = x 2 − 2 2 2 0 8 : 2 2 x y x D 将D = D1 + D2 D : 视为Y–型区域, 则 2 2y x 8 − y 0 y 2 = D I f (x, y)d x d y − 2 8 2 ( , )d y y f x y x = 2 0 dy

例4.计算1=∬Dxdo,其中D是直线y=1,x=2,及 y=x所围的闭区域 .1≤y≤x 解法1.将D看作X-型区域,则D1≤x≤2 I-dxddx 2 1 -I5x2-5]x8 ∫y≤x≤2012 解法2.将D看作Y-型区域,则D:1<y≤2 1-dx-ia-=l2y-8
山东农业大学 高等数学 主讲人:苏本堂 x y 2 1 1 y = x o 2 = 2 1 dy 例4. 计算 d , = D I xy 其中D 是直线 y=1, x=2, 及 y=x 所围的闭区域. x 解法1.将D看作X–型区域, 则 D : I = 2 1 d x xyd y = 2 1 d x = − 2 1 2 3 1 2 1 x x dx 8 9 = 1 2 2 1 x xy 解法2.将D看作Y–型区域,则 D : I = xyd x 2 1 d y y x y 2 2 2 1 = − 2 1 3 2 1 2y y dy 8 9 = y 1 x y 2 1 y x 1 x 2 y x 2 1 y 2

例5.计算 小Dxdo,其中D是抛物线y2=x及直线 y=x-2所围成的闭区域! 2 解:为计算简便,先对x后对y积分, 则 y=x-2 da-品d =2]ay-20+22-51ay +22-612
山东农业大学 高等数学 主讲人:苏本堂 例5. 计算 d , D xy 其中D 是抛物线 所围成的闭区域. 解: 为计算简便, 先对 x 后对 y 积分, D : xy d x D xyd − = 2 1 dy − + = 2 1 2 2 2 1 x y 2 dy y y − = + − 2 1 2 5 [ ( 2) ] d 2 1 y y y y D y = x 2 y = x − 2 2 −1 4 o y x y 2 2 y x y + −1 y 2 2 y y + 2 及直线 则