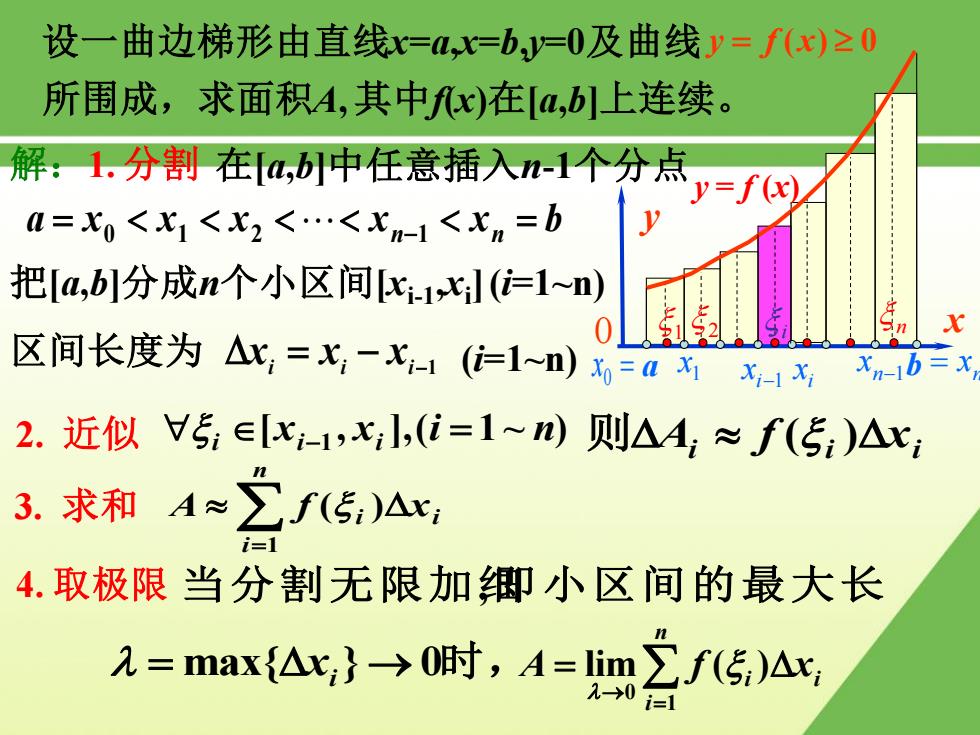
设一曲边梯形由直线c=4,x=b,y=0及曲线y=f(x)≥0 所围成,求面积A,其中fx)在,b]上连续。 解:1.分割在a,b小中任意插入n-1个分点 y=f(x) Q=X0<x1<x2<<X-1<x=b 把[a,b]分成n个小区间c.1l(=1) 0 区间长度为△x,=x,--1(=1)x三0x Xi-1xi Xn-1b= 2.近似5:∈x-1,x;,(i=1~m)则△4:≈f(5:)△x: 3.求和A≈∑f(传:)△x: f-1 4.取极限当分割无限加卿小区间的最大长 2=max{△;}→0时,A=lim∑f(5)△x, i-1
设一曲边梯形由直线x=a,x=b,y=0及曲线 解:1. 分割 a x x x x x b 0 1 2 n1 n 把[a,b]分成n个小区间[xi-1 ,xi ] (i=1~n) 区间长度为 i i i1 x x x (i=1~n) y f (x) 0 所围成,求面积A, 其中f(x)在[a,b]上连续。 2. 近似 [ , ],( 1 ~ ) i xi1 xi i n 3. 求和 i n i A f i x ( ) 1 0 x y a b y = f (x) 0 x 1x i i x x 1 n1 x n x 1 2 i n i i xi 则A f ( ) 4. 取极限 当分割无限加细,即小区间的最大长度 i n i A f i x lim ( ) 1 0 max{xi } 0时, 在[a,b]中任意插入n-1个分点

设一曲边梯形由直线x=a,x=b,=0及曲线y=f(x)≥0 所围成,求面积A,其中fx)在a,b]上连续。 解:1.分割在a,b中任意插入n-1个分点 y=f(x) 0=x0<X1<x2<<xm-1<xn=b 把a,b]分成n个小区间c1x(=1n) 区间长度为△x,=x,-x-1(=1~) 2.近似V5:∈x-1,:,(i=1~m)则△4:≈f(5:)△x 3.求和A≈∑f5)△x: i=1 4.取极限当分割无限加御小区间的最大长 2=max{△c}→0时,A=lim∑f(传)△ →0 i=1
设一曲边梯形由直线x=a,x=b,y=0及曲线 解:1. 分割 a x x x x x b 0 1 2 n1 n 把[a,b]分成n个小区间[xi-1 ,xi ] (i=1~n) 区间长度为 i i i1 x x x (i=1~n) y f (x) 0 所围成,求面积A, 其中f(x)在[a,b]上连续。 2. 近似 [ , ],( 1 ~ ) i xi1 xi i n 3. 求和 i n i A f i x ( ) 1 0 x y a b y = f (x) i i xi 则A f ( ) 4. 取极限 当分割无限加细,即小区间的最大长度 i n i A f i x lim ( ) 1 0 在[a,b]中任意插入n-1个分点 max{xi } 0时

实例2(求变速直线运动的路程) 设某物体作变速直线运动.已知速度V=(是 时间间隔[T,T上t的连续函数.计算在这段时间内 物体所经过的路程S. 匀速直线运动.路程=速度X时间 思路:把整段时间分割成若干小段,每小段上速度 看作不变,求出各小段的路程再相加,便得到路程 的近似值,最后通过对时间的无限细分过程求得路 程的精确值
设某物体作变速直线运动. 已知速度V = V(t)是 时间间隔[T1 , T2 ]上 t 的连续函数. 计算在这段时间内 物体所经过的路程 S. 匀速直线运动. 路程=速度×时间 实例2 (求变速直线运动的路程) 思路:把整段时间分割成若干小段,每小段上速度 看作不变,求出各小段的路程再相加,便得到路程 的近似值,最后通过对时间的无限细分过程求得路 程的精确值.