
第六章 定积分在几何中的应用 一、定积分的元素法 二、平面图形的面积 三、立体图形的体积 四、平面曲线的弧长
第六章 定积分在几何中的应用 一、定积分的元素法 二、 平面图形的面积 四、 平面曲线的弧长 三、 立体图形的体积
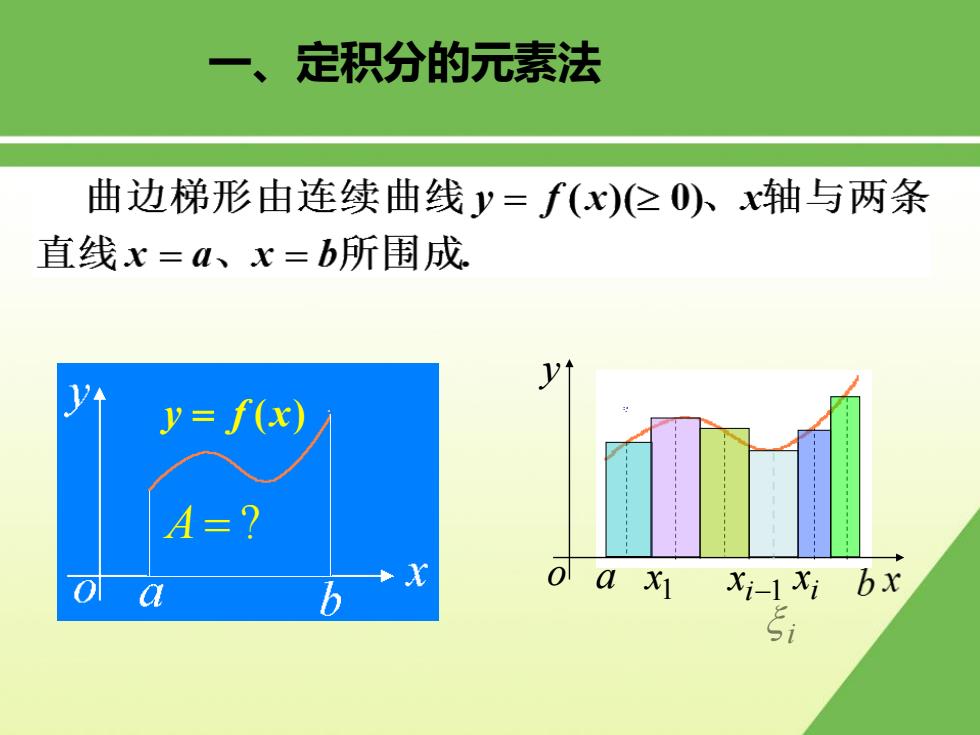
一、 定积分的元素法 曲边梯形由连续曲线y=f(x)≥0)、x轴与两条 直线x=a、x=b所围成 1) y=f(x) A=? 0a为1X-1X1bx Si
一、定积分的元素法 A ? y f (x) a y o 1x i x i1 x i

(1)分割: A=∑A4 (2)近似代替 △A≈f(5)△x (3)求和 4交M (4)取极限 4=交s)h
(1)分割: 1 n i i A A (2)近似代替 ( ) A f x i i i (3)求和 1 ( ) n i i i A f x (4)取极限 0 1 lim ( ) ( ) n b i i a i A f x f x dx

可以用定积分解决的问题 一般地,若某实际问题中的所求量U符合以下条件: (1)U是一个与变量x的变化区间[a,b]有关的量, (2) U关于区间具有可加性, (3) 部分量△U的近似值形如f(x)△x. 则可考虑用定积分来表达这个量U
(1) ; U x 是一个与变量 的变化区间[a,b]有关的量 则可考虑用定积分来表达这个量 U 一般地, 若某实际问题中的所求量 U 符合以下条件: (2) U ; 关于区间具有可加性 (3) ( ) . 部分量 U f x x i i i 的近似值形如 可以用定积分解决的问题

具体过程 ()根据实际问题,选取一个积分变量x,并确定其变化区间[a,b]; (2) 设想把[a,b]分成n个小区间,选取典型小区间[x,x+dx],求出此区间 上部分量△U的近似值△U≈f(x)dx,得到所求量U的元素dU=fx)dx (3)以所求量U的元素fx)为被积表达式,在区间[a,]上作定积分, 得到U的积分表达式U=∫fx)d,计算定积分得到量U 元素法
(2) 设想把 [ , ] , [ , d ], a b n x x x 分成 个小区间 选取典型小区间 求出此区间 得到 U 的积分表 ( )d , b a U f x x U 达式 计算定积分得到量 (1)根据实际问题, , [ , ] ; 选取一个积分变量 x a b 并确定其变化区间 上部分量 U U f x x U U f x x 的近似值 Δ ( )d , d ( )d 得到所求量 的元素 (3)以所求量 ( )d , [ , ] , U f x x a b 的元素 为被积表达式 在区间 上作定积分 具体过程 元素法