
第五节对坐标的曲面积分 一、对坐标的曲面积分的概念与性质 二、对坐标的曲面积分的计算法 三、两类曲面积分的联系
第五节 一、 对坐标的曲面积分的概念与性质 二、对坐标的曲面积分的计算法 三、两类曲面积分的联系 对坐标的曲面积分
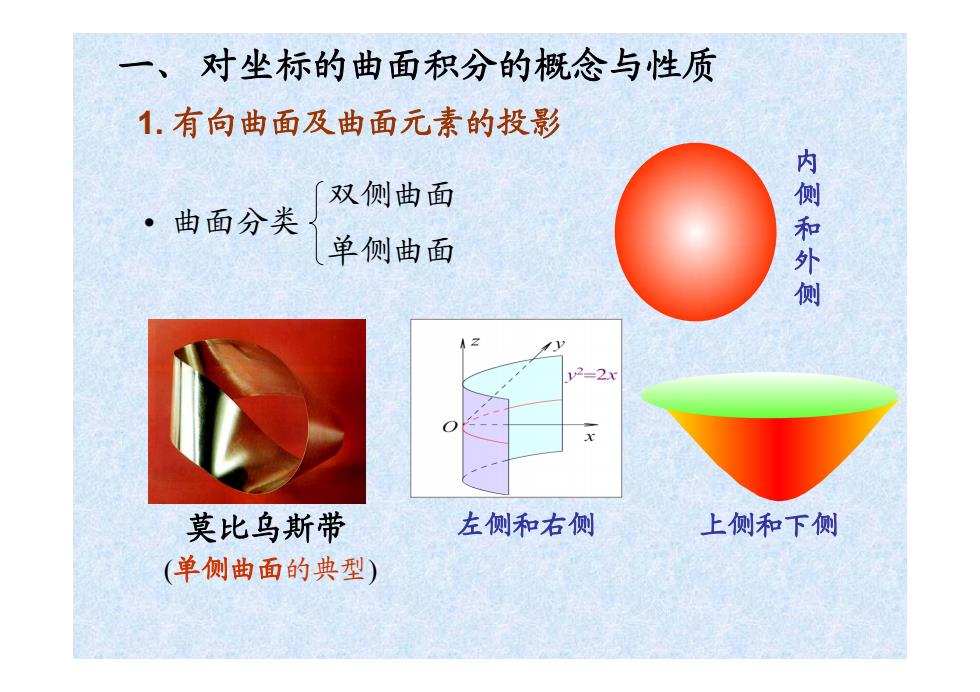
一、 对坐标的曲面积分的概念与性质 1.有向曲面及曲面元素的投影 双侧曲面 ·曲面分类 单侧曲面 内侧和外侧 w2=2x 0 莫比鸟斯带 左侧和右侧 上侧和下侧 (单侧曲面的典型)
1. 有向曲面及曲面元素的投影 • 曲面分类 双侧曲面 单侧曲面 莫比乌斯带 上侧和下侧 内 侧 和 外 侧 左侧和右侧 (单侧曲面的典型) 一 、 对坐标的曲面积分的概念与性质
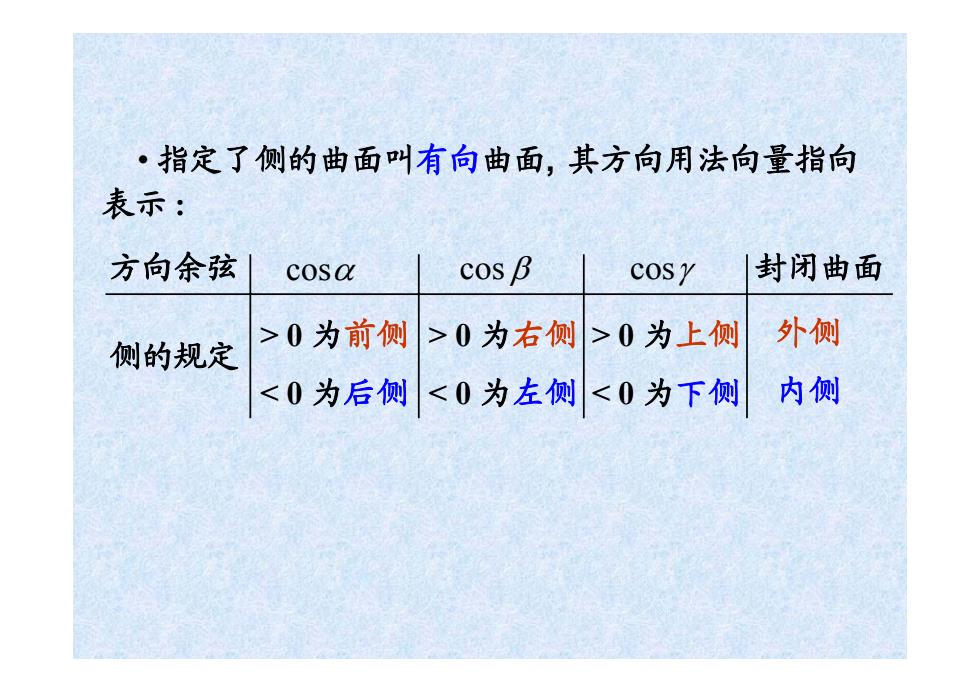
·指定了侧的曲面叫有向曲面,其方向用法向量指向 表示: 方向余弦 cosa cos B cosy|封闭曲面 外侧 侧的规定 >0为前侧>0为右侧>0为上侧 <0为后侧<0为左侧<0为下侧内侧
其方向用法向量指向 方向余弦 cosα cos β cosγ > 0 为前侧 < 0 为后侧 封闭曲面 > 0 为右侧 < 0 为左侧 > 0 为上侧 < 0 为下侧 外侧 内侧 侧的规定 • 指定了侧的曲面叫有向曲面, 表示 :

设∑为有向曲面,其面元△S在xOy面上的投影记为 (△S)xy,(AS)xy的面积为(△o)xy≥0,则规定 有向投影 (Ao)xy,当cosy>0时 (AS)xy=3-(AG)xy2 当cosy<0时 0, 当cosy=0时 类似可规定(AS)e,(AS)x
设 Σ 为有向曲面, ( ) , xy ΔS ΔS (ΔS) xy = 其面元 在 xOy 面上的投影记为 (Δ ) ≥ 0, S xy σ xy (Δ ) 的面积为 则规定 ( ) , Δσ xy ( ) , − Δσ xy 0 , 当cosγ > 0时 当cosγ < 0时 当cosγ ≡ 0时 有向投影 类似可规定 yz zx (ΔS) , (ΔS)

2.对坐标的曲面积分的概念 定义设∑为光滑的有向曲面,函数y,z在∑上有 界,把∑分成块小曲面△S,(△S,同时又表示第块小曲面 的面积),AS在x0y面上的投影为(AS)o,(5,n,5)是 △S;上任意取定的一点,如果当各小块曲面的直径的最大 值2→0时, im2R5,n-5aS),记作∬R(x,z)dd 2-→0 j=1 存在,则称此极限为函数R(x,y,z)在有向曲面∑上对坐 标x,y的曲面积分(也称第二类曲面积分) R(X,y,z):被积函数 ∑:积分曲面
2.对坐标的曲面积分的概念 定义 设Σ为光滑的有向曲面,函数 x y 在Σ上有 界,把Σ分成n块小曲面ΔSi(ΔSi同时又表示第 i块小曲面 的面积 ),ΔSi在xoy面上的投影为 Si xy (Δ ) , ( , , ) i i i ξ η ζ 是 ΔSi上任意取定的一点,如果当各小块曲面的直径的最大 λ →0 时, R( , ,z) 值 ∑ = → Δ n i R i i i Si xy 1 0 lim (ξ ,η ,ζ )( ) λ 存在, 则称此极限为函数R(x, y,z)在有向曲面Σ上对坐 标x, y的曲面积分(也称第二类曲面积分) ∫∫ Σ R(x, y,z)dxdy 记作 R(x, y,z):被积函数 Σ:积分曲面