
第九章多元函数微分法及其应用 一元函数微分学 推广 多元函数微分学
推广 第九章 一元函数微分学 多元函数微分学 多元函数微分法及其应用

第一节 多元函数的基本概念 一、区域 二、多元函数的概念 三、多元函数的极限 四、多元函数的连续性
第一节 一、区域 二、多元函数的概念 三、多元函数的极限 四、多元函数的连续性 多元函数的基本概念

一、区域 1.邻域 点集U(,δ)={PPP<6},称为点Po的6邻域. 例如,在平面上, U(,δ)={《x,y)V(x-x2+(y-%)2<6}(圆邻域) 在空间中, U(D,6)={(xy,zV(x-x)2+(y-%)2+(z-0)2<6} (球邻域) 说明:若不需要强调邻域半径6,也可写成U() 点Po的去心邻域记为U(P)={P0<PP<δ}
0 )( o PPU PP δ 0 0 一、 区域 1. 邻域 点集 , ),(PU 0 δ P 称为点 P0 的 邻域. 例如,在平面上, PU 0 δ yx ),(),( (圆邻域) 在空间中, 0 zyxPU ),,(),( (球邻域) 说明:若不需要强调邻域半径 ,也可写成 .)( U P0 点 P0 的去心邻域记为 PP δ 0 yyxx δ 2 0 2 0 )()( zzyyxx δ 2 0 2 0 2 0 )()()(
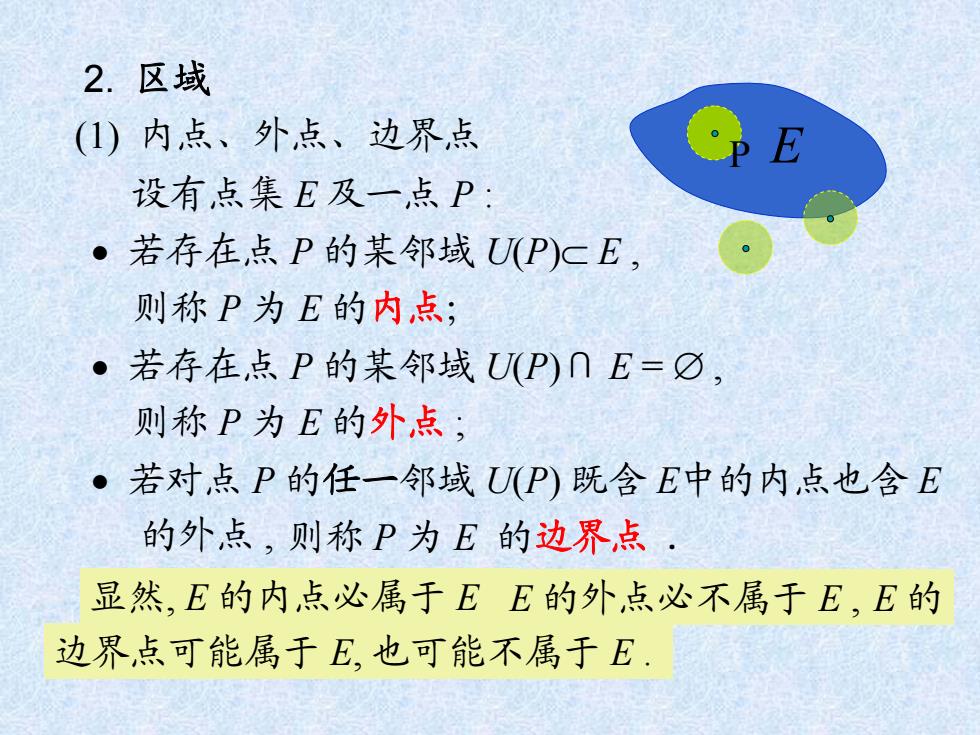
2.区域 (1)内点、外点、边界点 设有点集E及一点P: ·若存在点P的某邻域U(P)cE, 则称P为E的内点; ·若存在点P的某邻域U(P)∩E=☑, 则称P为E的外点; ·若对点P的任一邻域UP)既含E中的内点也含E 的外点,则称P为E的边界点 显然,E的内点必属于EE的外点必不属于E,E的 边界,点可能属于E,也可能不属于E
2. 区域 (1) 内点、外点、边界点 设有点集 E 及一点 P : 若存在点 P 的某邻域 U(P) E , 若存在点 P 的某邻域 U(P)∩ E = , 若对点 P 的任一邻域 U(P) 既含 E中的内点也含 E E 则称 P 为 E 的内点; 则称 P 为 E 的外点 ; 则称 P 为 E 的边界点 的外点 , . 显然, E 的内点必属于 E , E 的外点必不属于 E , E 的 边界点可能属于 E, 也可能不属于 E . P

(2)聚点 若对任意给定的δ,点P的去心 E 邻域U(P,δ)内总有E中的点,则 称P是E的聚点 聚点可以属于E,也可以不属于E(因为聚点可以为 E的边界,点)
(2) 聚点 若对任意给定的 ,点P 的去心 (PU δ), E 邻域 内总有E 中的点 , 则 称 P 是 E 的聚点. 聚点可以属于 E , 也可以不属于 E (因为聚点可以为 E 的边界点 )