
第一节向量及其线性运算 一、向量概念 二、向量的线性运算 三、空间直角坐标系 四、利用坐标作向量的线性运算 五、向量的模、方向角、投影
一、向量概念 二、向量的线性运算 四、利用坐标作向量的线性运算 三、空间直角坐标系 五、向量的模、方向角、投影 第一节 向量及其线性运算

一、向量概念 1、概念 (1)向量:既有大小又有方向的量。 如位移、速度、加速度、力、力矩等。,B (2)向量表示:用一条有向线段表示.ū (终点 (3)向量的模向量的大小. A (4)单位向量:模长为1的向量. (起点) (⑤)零向量模长为0的向量,记做0(方向是任意的) (6)自由向量:与起点无关的向量 (7)两向量的夹角: 6 p=位)=6,)0≤ps列 d
⑴向量:既有大小又有方向的量。 如位移、速度、加速度、力、力矩等。 ⑵向量表示:用一条有向线段表示. a 模长为1的向量. 模长为0 的向量,记做0 a || ⑶向量的模:向量的大小. 1、概念 ⑷单位向量: ⑸零向量: 一、向量概念 (6)自由向量:与起点无关的向量 A (起点) B (终点) (方向是任意的) (7)两向量的夹角: a b ba ),( ab ),( 0( )

2、两非零向量的关系 (1)相等:大小相等且方向相同的向量. 记a=b(平行移动后能完全重合) (2)平行:方向相同或相反的两个非零向量.记ā∥ 两向量平行也称为共线 (3)垂直:夹角为元的两个非零向量.记ā1石 注意:由于零向量的方向可以看成任意的,故零 向量与任何向量都平行或垂直。 (4)共面:把若千个向量的起,点放到一起,若它们的 终点和公共起点在同一平面上,则称这些 向量共面
2、两非零向量的关系 ⑴相等:大小相等且方向相同的向量. a b ba 记 ⑵平行:方向相同或相反的两个非零向量. ba 记 // 注意:由于零向量的方向可以看成任意的,故零 向量与任何向量都平行或垂直。 ⑷共面:把若干个向量的起点放到一起,若它们的 终点和公共起点在同一平面上,则称这些 向量共面. (平行移动后能完全重合) 两向量平行也称为共线. ⑶垂直: ba 夹角为 记 的两个非零向量. 2
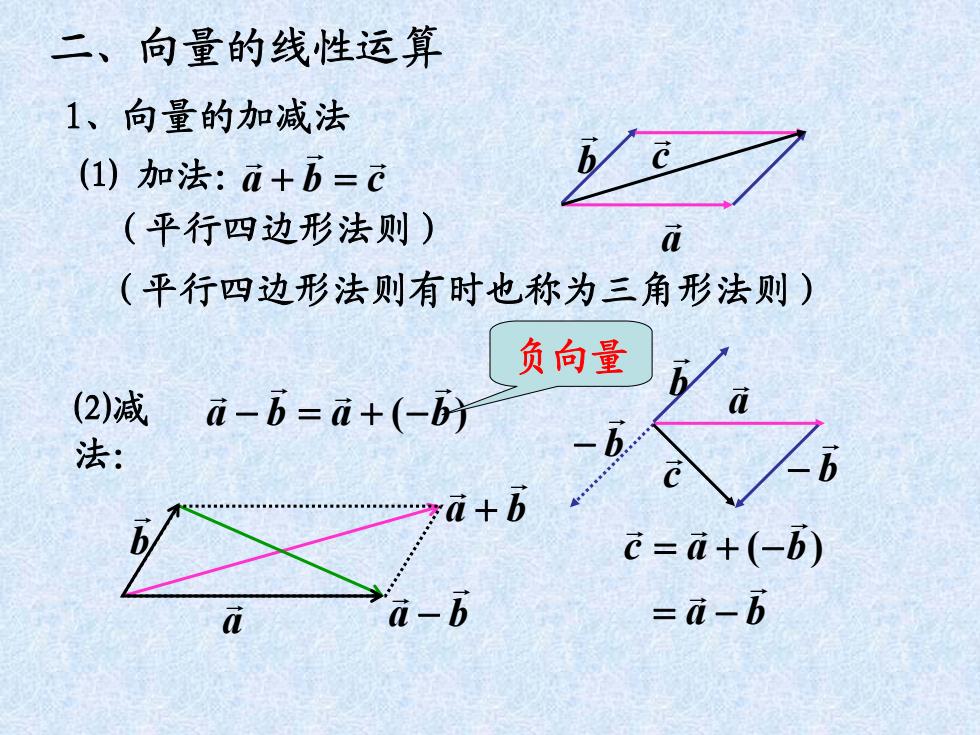
二、向量的线性运算 1、向量的加减法 (1)加法:a+b=c (平行四边形法则) d (平行四边形法则有时也称为三角形法则) 负向量 (2)减d-b=a+(-时 法: …学d+b c=d+(-b) a-b -a-b
⑵减 法: baba )( a b b b c ba bac )( ba ba a b 1、向量的加减法 ⑴ 加法: cba a b c (平行四边形法则) (平行四边形法则有时也称为三角形法则) 二、向量的线性运算 负向量

2、向量与数的乘法 (1)定义:向量a与实数1的乘积1d是一个新向量. i)2>0,2d与d同向,|2d=2| 2=0,a=0 ii地2<0,2d与d反向,|2i曰2ldl (2)单位向量的表示 向量的单位化 若a40,则有单位向量8- 因此a=lae
2、向量与数的乘法 i ,0) a 与 a 同向, aa |||| ii ,0) 0 a iii ,0) a 与 a 反向, aa |||||| ⑵单位向量的表示 a 0, , a a ea 则有单位向量 因此 . a eaa 若 向量的单位化 ⑴ 定义:向量 与实数 的乘积 a 是一个新向量. a