
第三节格林公式及其应用 一、格林公式 二、平面上曲线积分与路径无关的条件 三、二元函数的全微分求积
一、格林公式 二、平面上曲线积分与路径无关的条件 三、二元函数的全微分求积 第三节 格林公式及其应用
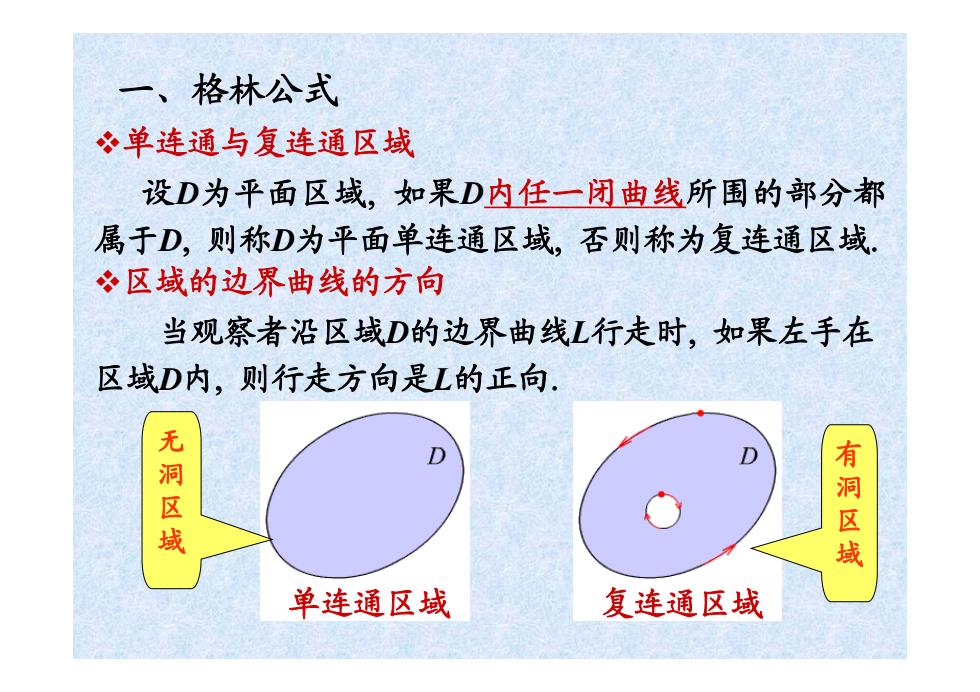
一、格林公式 ·单连通与复连通区域 设D为平面区域,如果D内任一闭曲线所围的部分都 属于D,则称D为平面单连通区域,否则称为复连通区域。 ?区域的边界曲线的方向 当观察者沿区域D的边界曲线L行走时,如果左手在 区域D内,则行走方向是L的正向 无洞区域 D D 有洞区域 单连通区域 复连通区域
一、格林公式 单连通与复连通区域 区域的边界曲线的方向 当观察者沿区域D的边界曲线L行走时, 如果左手在 区域D内, 则行走方向是L的正向. 单连通区域 复连通区域 设D为平面区域, 如果D内任一闭曲线所围的部分都 属于D, 则称D为平面单连通区域, 否则称为复连通区域. 无 洞 区 域 有 洞 区 域

必定理1 设闭区域D由分段光滑的曲线L围成,函数P,y及 2,以在D上具有一阶连续偏导数,则有 小器器hPh+0一格林公式 其中L是D的取正向的边界曲线: 注:格林公式反映的是二重积分和第二类曲线积 分的关系
∫∫ ∫ = + ∂∂ − ∂∂ L D dxdy Pdx Qdy y P x Q( ) , 定理1 设闭区域D由分段光滑的曲线L围成, 函数P(x, y)及 Q(x, y)在D上具有一阶连续偏导数, 则有 其中L是D的取正向的边界曲线. ——格林公式 注:格林公式反映的是二重积分和第二类曲线积 分的关系

证明:1)若D既是X型区域,又是Y型区域,且 p1(x)≤y≤p2(x) ↑y E d a≤x≤b 4(y)≤x≤W2(y) C c≤y≤d 2a,-装 则 -Q(v2().y)dy-[Q((y).y)dy -ae0xMy-∫cac(x,Hy =∫eQx,y+∫acx,y
证明: 1) 若D 既是 X 型区域 , 又是 Y 型区域 , 且 ⎩ ⎨ ⎧ ≤ ≤ ≤ ≤ a x b x y x D ( ) ( ) : ϕ1 ϕ 2 ⎩ ⎨ ⎧ ≤ ≤ ≤ ≤ c y d y x y D ( ) ( ) : ψ 1 ψ 2 则 x y x Q D d d ∫∫ ∂ ∂ ∫ = d c Q ( ( y), y ) d y ψ 2 ∫ ∂ ( ) ∂ ( ) 2 1 d y y x x ψ Q ψ ∫ = CBE Q ( x, y ) d y ∫ − CAE Q ( x, y ) d y ∫ = CBE Q ( x, y ) d y ∫ + EAC Q ( x, y ) d y ∫ − d c Q ( ( y), y ) d y ψ 1 ∫ = d c d y d c y o x E C A B a b D

即 儿器dd. ① 同理可证 -d-,a ② ①、②两式相加得: n是adv-fH+
即 x y x Q D d d ∫∫ ∂∂ ∫ = LQ(x, y)dy 同理可证 x y y P D d d ∫∫ ∂∂ − ∫ = L P(x, y)dx ① ② ①、②两式相加得: ( ) ∫∫ ∫ = + ∂∂ − ∂∂ D L x y P x Q y yP xQ d d d d