南阳师范学院：《高等数学》课程教学课件（同济第六版）第三章 微分中值定理与导数的应用 3.1 微分中值定理

第三章{ 微分中值定理与导数的应用 Bagrange 柯西，A.L 费马，P.de

第三章 微分中值定理与导数的应用

罗尔中值定理 推广 中值定理 拉格朗日中值定理 ◆泰勒公式 (第三节) 柯西中值定理 研究函数性质及曲线性态 应用 利用导数解决实际问题

中值定理 应用 研究函数性质及曲线性态 利用导数解决实际问题 罗尔中值定理 拉格朗日中值定理 柯西中值定理 泰勒公式 (第三节) 推广

第一节微分中值定理 一、 罗尔定理 二、拉格朗日中值定理 三、柯西中值定理

一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 第一节 微分中值定理

一 罗尔定理 1.费马引理 (1)函数fx)在点x,的某邻域U(x)内有定义，且在点x处可导； (2)对任意的x∈Ux,).有f(x)≤f(xo)(或f(x)≥f(xo), 则 f'(x)=0 导数为零的点称为函数的驻点（或称稳定点，临界点）

1. 费马引理 （2）对任意的 0 x x  ( ) ， 有 ( ) ( )  ( ) ( ), 0 0 f x  f x 或 f x  f x 则 （1）函数 f x( )在点 0 x 的某邻域 0 U x( )内有定义，且在点 0 x 处可导; 0 f x ( ) 0  一、罗尔定理 导数为零的点称为函数的驻点（或称稳定点，临界点）

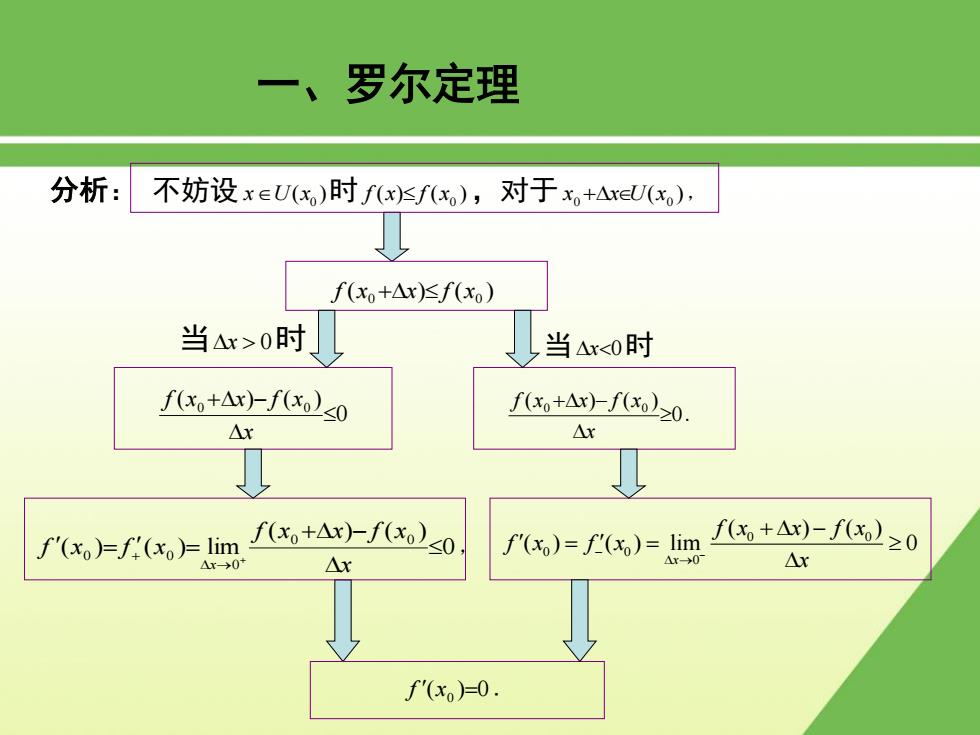
一、罗尔定理 分析：不妨设x∈Ux,)时,),对于+AxeU), f(xo+Ax)f(xo) 当△x>0时 当Ar<0时 fx+△xfxo)0 f(xo+Ax)-f(xo)20. △x △x f'(xo)=f (xo)=lim f(xo+Ax)-f(xo)20 fx,)=fx)=imf+A)-f≥0 Aro △x→0 △x △x f'(x)=0

( ) ( ) 0 0 f x x  f x 分析： 不妨设 0 x U x  ( )时 ( ) ( ) 0 f x  f x ，对于 ( ) 0 0 x xU x ， 0 ( ) ( ) 0 0     x f x x f x 0 ( ) ( ) ( ) ( ) lim 0 0 0 0 0             x f x x f x f x f x x ， 一、罗尔定理 0 0 0 0 0 ( ) ( ) ( ) ( ) lim 0 x f x x f x f x f x x              0 ( ) ( ) 0 0     x f x x f x . f (x0 )0 . 当 x 0时 当x0时