
第十一章 曲线积分与曲面积分 积分学 定积分二重积分三重积分曲线积分曲面积分 积分域 区间 平面域 空间域 曲线孤 曲面域 对孤长的曲线积分 曲线积分 对坐标的曲线积分 对面积的曲面积分 曲面积分 对坐标的曲面积分
第十一章 积分学 定积分二重积分三重积分 积分域 区 间 平面域 空间域 曲线积分 曲线弧 曲面域 曲线积分 曲面积分 对弧长的曲线积分 对坐标的曲线积分 对面积的曲面积分 对坐标的曲面积分 曲面积分 曲线积分与曲面积分

第一节对孤长的曲线积分 一、对孤长的曲线积分的概念与性质 二、对孤长的曲线积分的计算法
第一节 一、对弧长的曲线积分的概念与性质 二、对弧长的曲线积分的计算法 对弧长的曲线积分
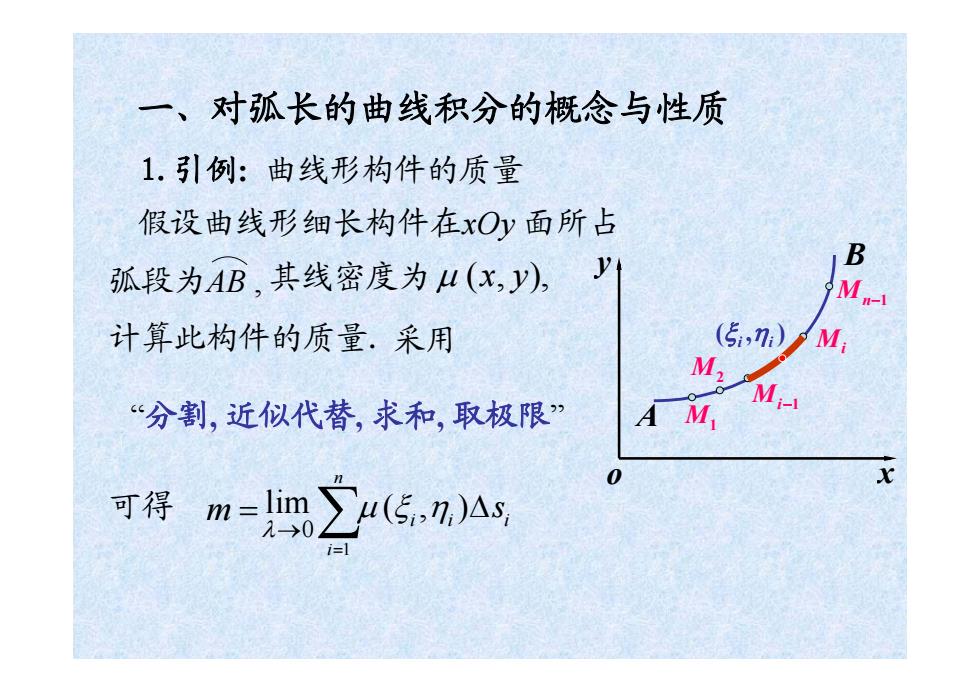
一、对孤长的曲线积分的概念与性质 1.引例:曲线形构件的质量 假设曲线形细长构件在xOy面所占 y B 孤段为AB,其线密度为u(x,y) M 计算此构件的质量.采用 (5,n)M M22 “分割,近似代替,求和,取极限” A M 可得m=∑4(5nA
一、对弧长的曲线积分的概念与性质 假设曲线形细长构件在xOy 面所占 弧段为AB , 其线密度为 μ ( , ), x y “分割, 近似代替, 求和, 取极限” (, ) ii i 可得 μ ξ η Δ s 1 n i= m = λ lim → 0 ∑ 计算此构件的质量. 1.引例 : 曲线形构件的质量 采用 o x y A B Mn − 1 Mi Mi− 1 M2 M1 ( , ) ξ i ηi

2.定义 设L是xOy面中一条光滑的曲线孤,函数f(x,y)是定 义在L上的一个有界函数,若通过对L的任意分割和对 局部的任意取点,下列“乘积的和式极限” 立w 积分孤段 被积函数 都存在,则称此极限为函数f(x,y)在曲线孤L上对孤长 的曲线积分,或第一类曲线积分
设 L是xOy 面中一条光滑的曲线弧,函数 是定 义在 L上的一个有界函数, 都存在, f (, ) x y 的曲线积分, = 记作 ( , )d L f xy s ∫ 若通过对 L的任意分割 局部的任意取点, 2.定义 f (, ) x y 下列“乘积的和式极限” 则称此极限为函数 在曲线弧L上对弧长 或第一类曲线积分. 积分弧段 被积函数 0 lim λ→ 和对 (, ) ii i f ξ η Δs 1 n i= ∑

曲线形细长构件的质量 m=2(5,nA=∫4(xnds i= 注:1.若函数f(x,y)在光滑的曲线孤L上连续,则 ∫fcd娱存在的 2.如果L是闭曲线,则记为f,fx,)ds 推广:/xyds=m2/5m,5 其中厂是空间曲线孤
( , )d L = μ xy s ∫ 曲线形细长构件的质量 (, ) ii i μ ξ η Δs 1 n i= m =λlim→0∑ 注:1.若函数 f (, ) x y 在光滑的曲线弧L上连续,则 ( , )d L f xy s ∫ 是存在的. 推广: f (, ,) x y z ds ∫Γ i ( , , )Δs i i i ∑ f ξ η ζ =ni 1 0 lim→ = λ 其中 Γ 是空间曲线弧. 2.如果 L 是闭曲线 , 则记为 ( , )d . ∫L f x y s