
1.2事件的频率与概率事件的频率1定义1:在相同条件下,进行n次试验,事件A发生n次,则称比值"为事件A 发生的频率,记作 f.(A),即 f.(A)="41频率满足下述三条基本性质(非负性)110≤f,(A)≤12、(规范性)f,(Q)=13、(有限可加性)对两两互不相容事件A,A,.,A,有:f.(ZA)-Zf.(A)i=-1i-l(NKD)Probability and Statistics
Probability and Statistics (NKD) 1.2 事件的频率与概率 一、事件的频率 , , , ( ). ( ) A A A n n n A n n n A f A f A n n = 在相同条件下 进行 次试验 事件 发生 次,则 称比值 为事件 发生的频率 记作 即 定义1: 频率满足下述三条基本性质: 0 1 n 1、(非负性) f ( A ) 2、(规范性) 1 n f ( ) = 3、(有限可加性)对两两互不相容事件 A ,A ,.,A 1 2 n 有: 1 1 n n n i n i i i f ( A ) f ( A ) = = =

注:频率一定程度上可以表示事件A发生的可能性的大小但由于它的波动性,用其表示事件A发生的可能性(概率)是不合适的,但通过试验我们发现:频率具有稳定性。具体地说:当试验次数n逐渐增大时,频率fn(A)呈现出稳定性例考虑“抛硬币”这个试验,考虑正面发生的事件为A,我们将一枚硬币抛5次,50次,500次,各做10遍,用表示事件A发生的次数f(A)表示A发生的频率,则得到的数据如表1.1所示。这样的试验在历史上也有不少人做过其中最著名的结果见表1.2NKDProbabilityand Statistics
Probability and Statistics (NKD) 注:频率一定程度上可以表示事件A发生的可能性的大小, 但由于它的波动性,用其表示事件A发生的可能性(概率) 是不合适的,但通过试验我们发现:频率具有稳定性。 具体地说:当试验次数n逐渐增大时,频率 f ( A ) n 呈现出稳定性. n f ( A ) A n 例 考虑“抛硬币”这个试验,考虑正面发生的事件为A,我们 将一枚硬币抛掷5次,50次,500次,各做10遍,用 表示事件A发生的次数, 如表1.1所示。这样的试验在历史上也有不少人做过, 其中最著名的结果见表1.2 表示A发生的频率,则得到的数据
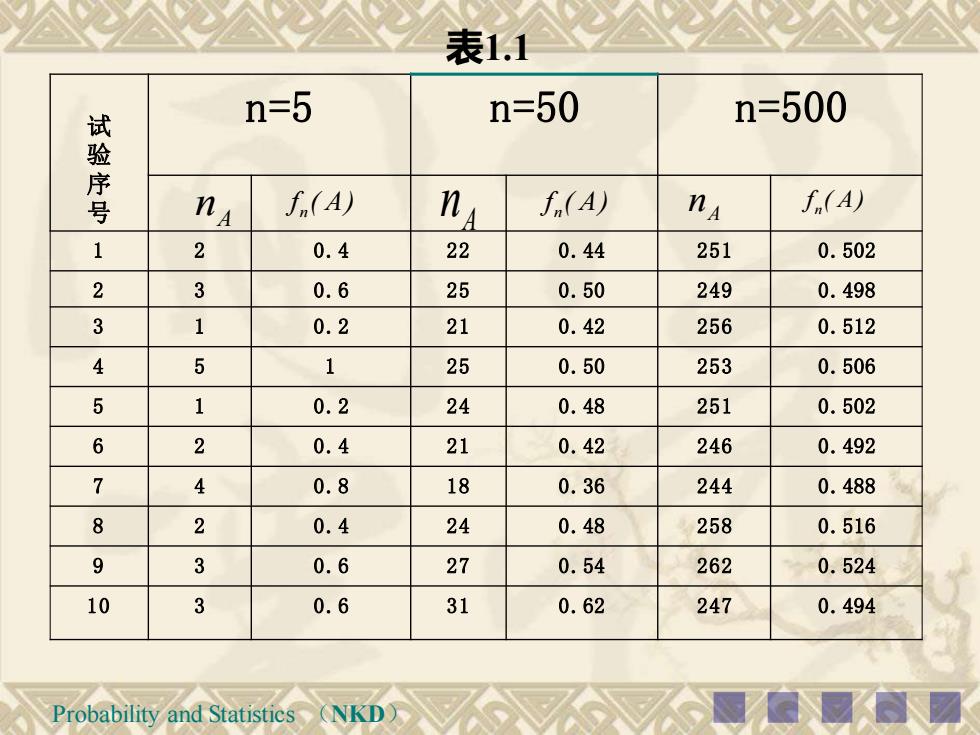
表1.1n=5n=50n=500试验序号nsf.(A)f.(A)nsf.(A)ns12220.40.442510.50223250.60.502490.49831210. 22560. 420.512541250.502530.50651240. 20. 482510.50262210. 40. 422460.49274180. 80. 362440.48882240. 40. 482580.51693270.60. 542620.524310312470. 60. 620. 494(NKD)Probability and Statistics
Probability and Statistics (NKD) A n n f ( A ) A f ( A ) n n A f ( A ) n n 试 验 序 号 n=5 n=50 n=500 1 2 0.4 22 0.44 251 0.502 2 3 0.6 25 0.50 249 0.498 3 1 0.2 21 0.42 256 0.512 4 5 1 25 0.50 253 0.506 5 1 0.2 24 0.48 251 0.502 6 2 0.4 21 0.42 246 0.492 7 4 0.8 18 0.36 244 0.488 8 2 0.4 24 0.48 258 0.516 9 3 0.6 27 0.54 262 0.524 10 3 0.6 31 0.62 247 0.494 表1.1

表1.2试验者NAf.(A)n德摩根204810610.5181蒲丰404020480.5069皮尔逊1200060190.5016皮尔逊24000120120.5005从试验中可以看出:当试验次数n逐渐增大时,A事件发生的频率越来越稳定在0.5数值周围.因此0.5可表示事件A发生的概率。以上表达了概率的统计性的定义,但要从频率直接获得概率确实非常困难的,甚至是不可能的。但我们可以从中提炼出概率的基本性质,从而给出概率的定义(NKDProbabilityand Statistics
Probability and Statistics (NKD) 试验者 德摩根 蒲 丰 皮尔逊 皮尔逊 n nA f (A) n 2048 1061 0.5181 4040 2048 0.5069 12000 6019 0.5016 24000 12012 0.5005 表1.2 从试验中可以看出:当试验次数n逐渐增大时,A事件 发生的频率越来越稳定在0.5数值周围.因此0.5可表示事件A 发生的概率。以上表达了概率的统计性的定义,但要从频率 直接获得概率确实非常困难的,甚至是不可能的。但我们可 以从中提炼出概率的基本性质,从而给出概率的定义

、概率的公理化定义定义2:设Q为试验E的样本空间.Q的子集A是随机事件,P(A)为实值函数,如果P(A)满足下述三条公理:1.(非负性)VA,有P(A)≥02.(规范性)对于必然事件2,有P(Q)=13.(完全可加性)对可列个两两互不相容的事件A,A,A…有: f,(ZA)=Zf.(A)l则称P(A)为随机事件A的概率,记作P(A)NKDProbabilityand Statistics
Probability and Statistics (NKD) 二、概率的公理化定义 定义2: 设Ω为试验 E 的样本空间, Ω 的子集 A 是随机事 件, P(A)为实值函数 ,如果 P(A) 满足下述三条公理: 2 3 k 1 1 1 P(A) 0 2. ( ) n i n i i i .( A, A ,A ,A ,.,A ., : f ( A ) f ( A ) ( A ) A , = = = 1 非负性) 有 规范性 对于必然事件 ,有P( )=1 3.(完全可加性)对可列个两两互不相容的事件 有 则称P 为随机事件 的概率 记作P(A)