《概率论与数理统计》课程教学课件（PPT讲稿）第三章 随机向量及其分布 3.2 边缘分布

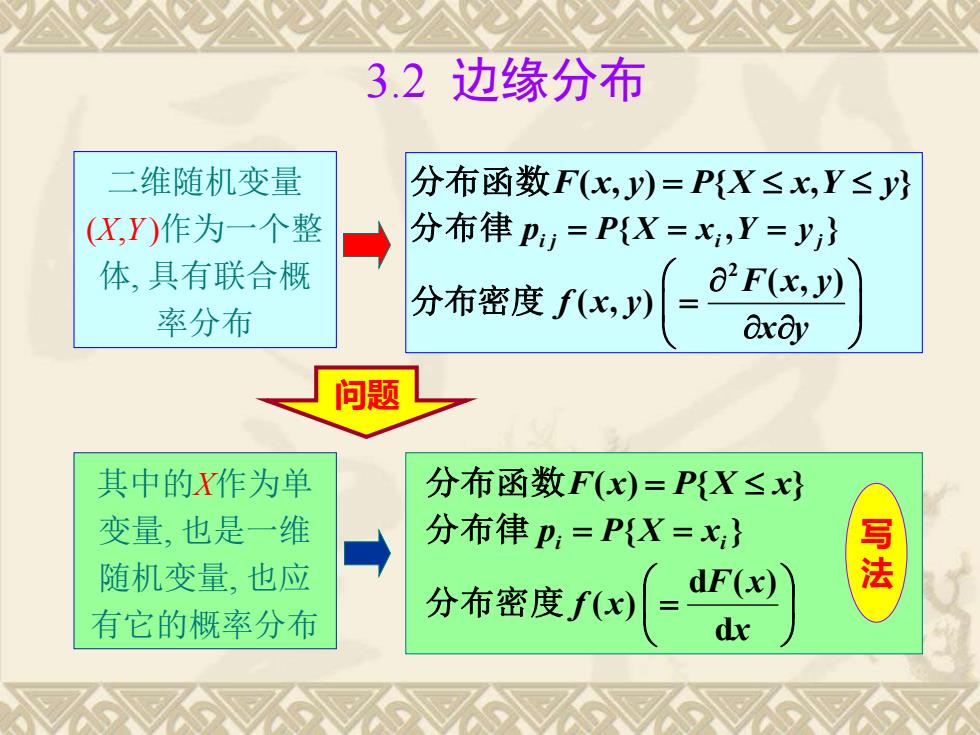
边缘分布3.2二维随机变量分布函数F(x,)=P[X≤x,Y≤(X,Y)作为一个整分布律pi,=P(X=x,,Y=y,}体，具有联合概aF(x,y)分布密度f(x,y)率分布axay问题其中的X作为单分布函数F(x)=PX≤x)变量，也是一维分布律p=PX=x}写法随机变量，也应dF(x)分布密度f(x)有它的概率分布dx

3.2 边缘分布 二维随机变量 (X,Y)作为一个整 体, 具有联合概 率分布 分布函数F(x, y) = P{X  x,Y  y} { , } i j i j 分布律 p = P X = x Y = y 2 ( , ) ( , ) F x y f x y x y      =     分布密度 其中的X作为单 变量, 也是一维 随机变量, 也应 有它的概率分布 分布函数F(x) = P{X  x} { } 分布律 pi = P X = xi       = x F x f x d d ( ) 分布密度 ( ) 问题 写 法

设二维随机变量(X,Y)的联合分布函数为F(x,y) = P(X≤x,Y ≤y)则F(x) = P[X≤x) =P[X≤x,Y<+00) = F(x,+00)X的F,(y) = P(Y ≤ y) = P(X<+00, Y≤ y}= F(+00, y)Y的设二维离散型随机变量的联合分布律为Pij = P(X = X,,Y = y,} (i, j= 1,2,...)则Pi. = P[X = x,}= P(X = x,Y<+00)X的分布律0p(X = x,Y = y;=-Zpi, (i =1,2,..)j=li=Y的分布律P., = P(Y = y,}= P(X < +o0,Y = y,)Zp(X = x,Y = y,}= Epi, (j =1,2,.)福i=l

F(x, y) = P{X  x,Y  y} 设 则 F ( x) = P{X  x} = F(x,+ ) F ( y) = P{Y  y} = F(+ , y) X Y p = P{X = x ,Y = y } (i, j = 1,2, ) i j i j 设二维离散型随机变量的联合分布律为 i 则 p { } = P X = xi   = = j 1 pi j  (i = 1,2, )  = = = = 1 { , } j i j P X x Y y { }j = P Y = y   = = i 1 pi j  ( j = 1,2, )  = = = = 1 { , } i i j P X x Y y = P{X  x,Y  + } = P{X  + ,Y  y} = P{X = x ,Y  + } i  { , }j p j = P X  +  Y = y  二维随机变量(X,Y )的联合分布函数为 X 的 Y 的 Y 的分布律 X 的分布律

MP(X = x,}= Pi. =(X,Y)的分布律：Pu (i=- 1,2,...j=1Yyiy2P(X = x;}VXXiPrjP11P12PrP2.2P21P22P2j...00·PiPilPi2XiPij·000.00.1PY = y;)p.1p.2DP[Y = y,} = P., =EPi (j = 1,2,)边缘分布律i=l

X Y y1 y2  y j    xi x x 2 1 p1 1 p12  p1 j  p21 p2 2  p2 j     pi1 pi 2  pi j     (X,Y )的分布律：   = = = • = 1 { } j P X xi pi pi j   = = = • = 1 { } i j p j pi j P Y y  P{Y = y j }  { }i P X = x 1 边缘分布律  p1• p2• pi• p•1 p•2 p• j  ( j = 1,2, ) (i = 1,2, )

设二维随机变量(X,Y)的联合分布函数为 F(x,y)则F(x) = P(X≤x)= F(x,+00)边缘分布函数F(y) = P(Y ≤ y)= F(+00, y)设二维离散型随机变量的联合分布律为 Pij则Pi. = P(X = x,}= Epu,(i= 1,2,)j=1边缘分布律P.j = P(Y = yi} - Zpi,(j = 1,2,..)i=1设二维连续型随机变量的联合密度为f(x,y)则 fx(x)=ft f(x,y)d y边缘分布密度fr(y)= f f(x, y)dx

F(x, y) 设二维离散型随机变量的联合分布律为 则 i p { }i = P X = x   = = j 1 pi j (i = 1,2, ) { }i = P Y = y   = = i 1 pi j ( j = 1,2, )  p j 设二维随机变量(X,Y)的联合分布函数为 pi j f (x, y) 则 f X (x) = +  − f (x, y)d y f Y ( y) = 设二维连续型随机变量的联合密度为 边缘分布律  +  − f (x, y)d x 边缘分布密度 边缘分布函数 则 F ( x) = P{X  x}= F(x,+ ) F ( y) = P{Y  y} = F(+ , y) X Y

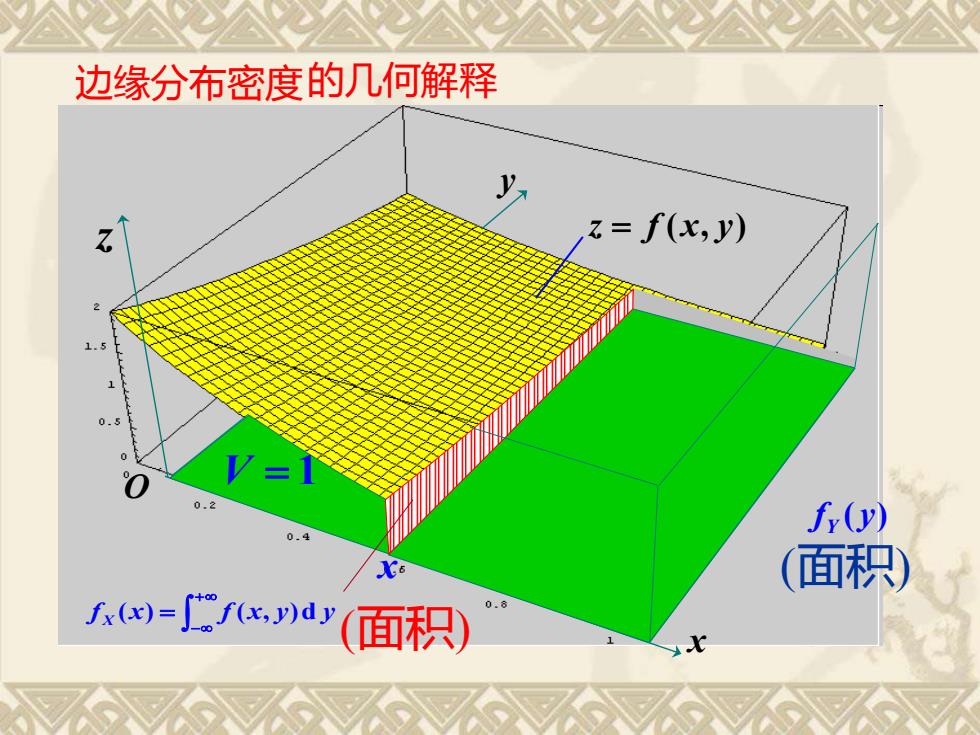
边缘分布密度的几何解释z= f(x,y)1.510.5o0.2fr(y)0.4（面积）0fx(x) = J f(x,y)dy(面积）

边缘分布密度 y x  +  − f x = f x y y X ( ) ( , )d f ( y) Y (面积) x 的几何解释 (面积) V = 1 z = f (x, y) O z