《概率论与数理统计》课程教学课件（PPT讲稿）第四章 随机变量及其数值模拟 4.2 二维随机变量函数的分布

4.2 二维随机变量函数的分布设(X,Y）是分布已知的二维随机变量，g(x，y)是二元连续函数，那么Z一g(X,Y)就是一个一维随机变量.按定义，随机变量Z=g(X,Y)的分布函数应为Fz(z)=P(Z≤z) =Pig(X,Y)≤z)本节讨论如何由已知的二维随机变量（X,Y的分布去求它的函数 Z=g(X,Y)的分布．特别如函数形式: Z=X±Y,Z=max(X,Y),Z=min(X,Y)

本节讨论如何由已知的二维随机变量(X,Y)的 分布去求它的函数 Z＝g(X,Y)的分布．特别如函 数形式： 设(X,Y )是分布已知的二维随机变量, g(x, y)是 二元连续函数, 那么Z＝g(X,Y)就是一个一维随机变 量. 按定义, 随机变量 Z＝g(X,Y)的分布函数应为 4.2 二维随机变量函数的分布 F (z) P{Z z} P{g(X,Y) z} Z =  =  Z X Y Z X Y Z X Y =  = = , max( , ), min( , )

例1 设(X,Y)的分布律Y0-1X1如右，求X+Y，max(X,Y)0.20.10与min(X,Y)的分布律0.20.10.10.3助

例1 设(X, Y)的分布律 如右, 求X+Y, max(X,Y ) 与min(X,Y )的分布律. Y X －1 0 1 0 0.1 0.2 0.2 1 0.1 0.1 0.3

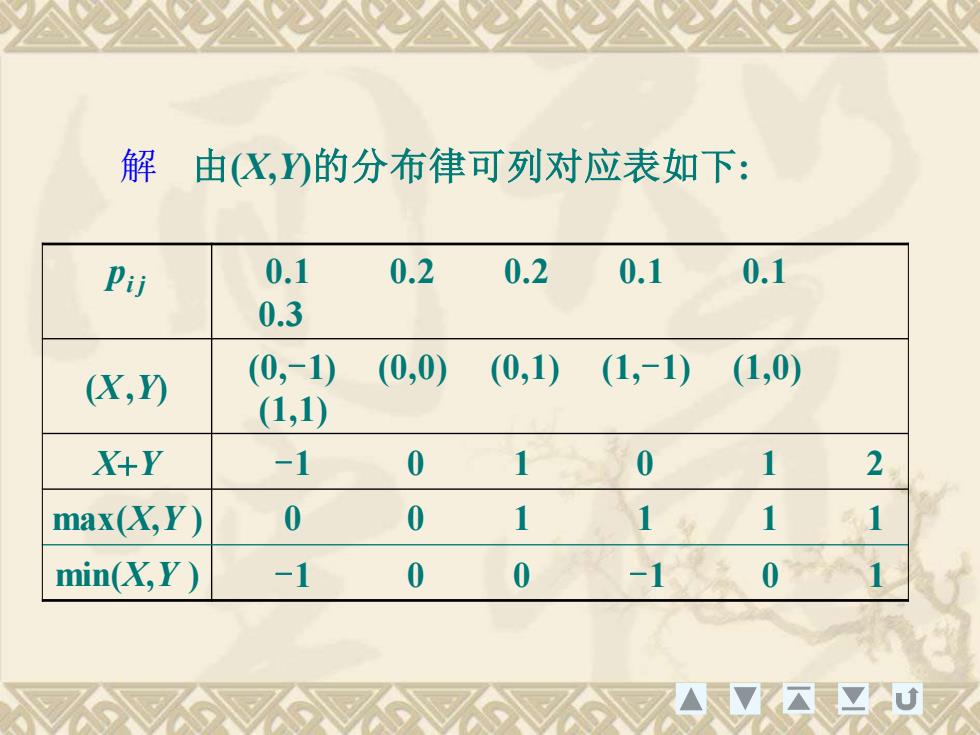
解日由(X,Y)的分布律可列对应表如下：0.20.10.20.10.1Pij0.3(0,0)(0,1)(1,0)(0,-1)(1,-1)(X,n)(1,1)0X+Y-1020011max(X,Y)0-10min(X,Y)1动

由(X,Y)的分布律可列对应表如下: pi j 0.1 0.2 0.2 0.1 0.1 0.3 (X,Y) (0,-1) (0,0) (0,1) (1,-1) (1,0) (1,1) X+Y -1 0 1 0 1 2 max(X,Y ) 0 0 1 1 1 1 min(X,Y ) -1 0 0 -1 0 1 解

将函数的所有可能取值重排并概率即可得分布律02X+Y0.10.30.30.30max(X,Y)0.30.701-1min(X,Y)0.20.50.3

分布律      − 0.2 0.5 0.3 1 0 1 min( X,Y ) ~       0.3 0.7 0 1 max( X,Y ) ~      − + 0.1 0.3 0.3 0.3 1 0 1 2 X Y ~ 将函数的所有可能取值重排并概率即可得

例2设两个独立的随机变量X与Y的分布律为3241YXp.jPi.0.30.70.60.4求随机变量Z-X+Y的分布律解 因X与Y独立,所以 P(X=X,Y=y;}= Pi。PijP(X=X,Y =y;}0.180.120.420.28(X,Y)(1, 2)(1, 4)(3, 2)(3, 4)3557Z=X+Y537Z=X+Y所求分布律P(Z = zk)0.540.180.28U

设两个独立的随机变量X 与Y 的分布律为 求随机变量 Z=X+Y 的分布律. i j i j P X x Y y p p • • 解 因X与Y 独立, 所以 { = , = } =  例2 X pi• 1 3 0.3 0.7 Y 2 4 j 0.6 0.4 p• (X,Y ) 0.18 0.12 0.42 0.28 Z = X +Y 3 5 5 7 Z = X +Y { }k P Z = z 3 5 7 0.18 0.54 0.28 所求分布律： { , } i j P X = x Y = y (1, 2) (1, 4) (3, 2) (3, 4)