《概率论与数理统计》课程教学课件（PPT讲稿）第二章 随机变量及其分布 2.2 离散型随机变量的概率分布

1.2离散型随机变量的概率分布一.离散型随机变量及分布律定义1.定义：如果随机变量X仅可能取有限个或可列无限多个值，则称X为离散型随机变量

1.2 离散型随机变量的概率分布 一.离散型随机变量及分布律定义： 1.定义：如果随机变量 X 仅可能取有限个或可列 无限多个值，则称 X 为离散型随机变量．

2.定义：设离散型随机变量X的所有可能的取值为x,(k =1,2,)，x 取各个可能值的概率为P(X = x,) = Pk, (k = 1,2,..) (2.1)由概率的定义，P，满足如下两个条件1° pk ≥ 0, (k =1,2,...) (2.2)人2°Z=1(2.3)Pkk=1称（2.1）式为离散型随机变量 X的分布律

2 1 (2.3) 1 0, ( 1,2, ) (2.2) 1 0 0 =  =   k= k k p p k  2.定义：设离散型随机变量 X 的所有可能的取值 为 x (k = 1,2, ), k X 取各个可能值的概率为 PX = x  = p , (k = 1,2, ) (2.1) k k 由概率的定义， pk满足如下两个条件 称（2.1）式为离散型随机变量 X 的分布律

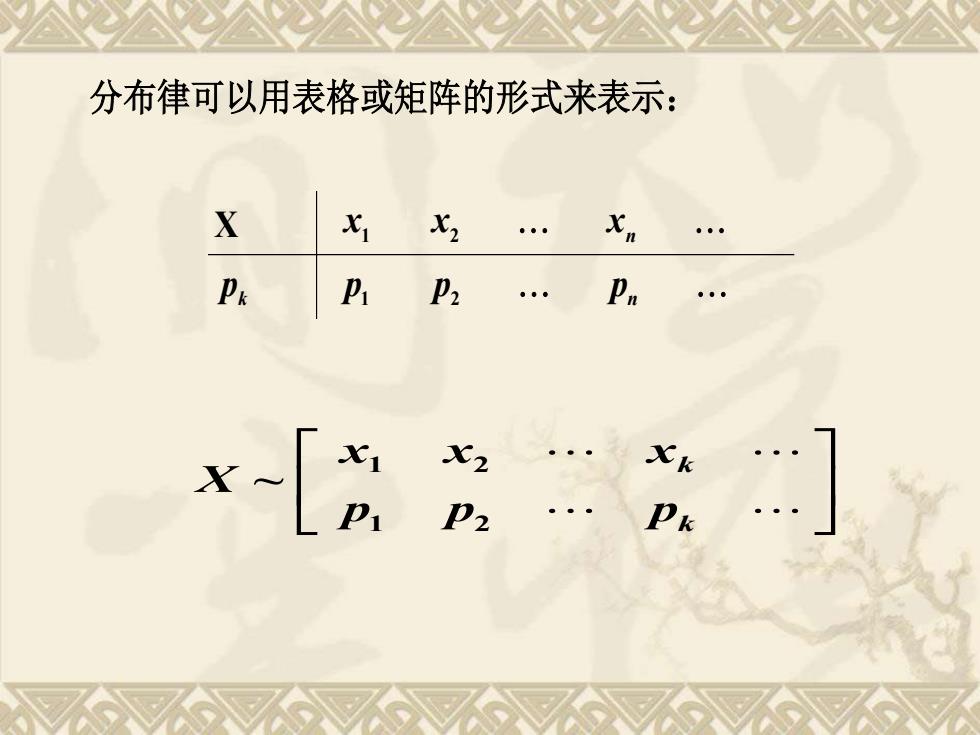
分布律可以用表格或矩阵的形式来表示：XxxX1PkPnPiP2xiX2XkX.piP2Pk

分布律可以用表格或矩阵的形式来表示： X x1 x2  xn  k p p1 p2  pn            k k p p p x x x X 1 2 1 2 ~

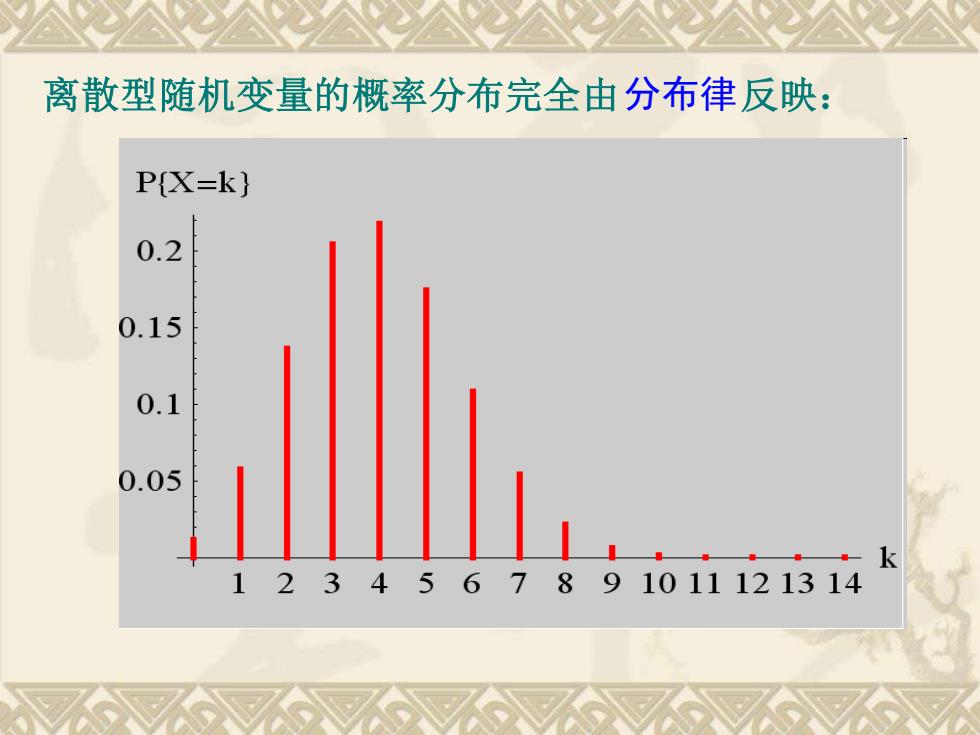
离散型随机变量的概率分布完全由分布律反映P(X-k)0.20.150.10.05112.1314

离散型随机变量的概率分布完全由分布律反映：

二.分布律性质：性质1: pk ≥0,k = 1,2,3...性质2：Zpk=1k=1三.分布率与分布函数间的关系F(x)= P(X≤x) = ZP(X =x}= ZPk;XSxX<xP(X = x) = F(x)- F(x -0)

二.分布律性质： p 0,k 1,2,3,. k  = p 1 k 1  k =  = 性质1: 性质2: 三.分布率与分布函数间的关系： { } ( ) ( ) ( ) { } { } ; = = − − 0 =  =  = =    k k k x x k x x k P X x F x F x F x P X x P X x p k k