
1.5随机事件的独立性直观的讲:事件A与事件B相互独立就是A事件发生的概率与B事件与否无关.即(A)= P(A|B)=P(A|B),由此得到: P(AB)= P(A)P(B) ,P(AB)=P(A)P(B)例如:甲乙两人投中篮球的概率分别为:0.6、0.7,我们知道"甲投中”与“乙投中相互独立,甲乙都投中的概率应为:0.6*0.7=0.42定义:若P(AB)=P(A)P(B)成立,则称事件A与事件B相互独立注:1、事件A与事件B的独立经常根据实际问题而判定2、“A与B独立”“A与B不相容”的关系:A与B不相容A与B不独立(相依)3、 A与B独立 A与B独立 A与B独立 A与B独立
1.5 随机事件的独立性 直观的讲:事件A与事件B相互独立就是A事件发生的概率 与B事件与否无关.即: 由此得到: ( ) ( ) ( ) , ( ) ( ) ( ). P AB P A P B P AB P A P B = = P A P A B P A B ( ) ( | ) ( | ), = = 例如:甲乙两人投中篮球的概率分别为:0.6、0.7,我们知道 “甲投中”与“乙投中”相互独立,甲乙都投中的概率应为: 0.6*0.7=0.42 定义:若P AB P A P B ( ) ( ) ( ) A B = 成立,则称事件 与事件 相互独立. 注:1、 事件A与事件B 的独立经常根据实际问题而判定. 2、 “A与B独立”“A与B不相容”的关系: A与B不相容 A与B不独立(相依) 3、 A B A B A B A B 与 独立 与 独立 与 独立 与 独立

证明:只证A与B独立三A与B独立P(AB)= P(A- AB)= P(A)- P(AB)= P(A)- P(A)P(B)= P(A)[1- P(B)) = P(A)P(B)因此:A与B独立定义: 设A,B,C三个事件,满足P(AB)= P(A)P(B),P(AC)=P (A) P (C), P(BC)= P(B)P(C)及P(ABC) = P(A)P(B)P(C) ,则称事件A,B,C相互独立注:三个事件中的任意两个都相互独立,不可得这三个事件相互独立
证明:只证A B A B 与 独立 与 独立 P AB P A AB P A P AB P A P A P B ( ) ( ) ( ) ( ) ( ) ( ) ( ) = − = − = − = − = P A P B P A P B ( )[1 ( )] ( ) ( ) 因此:A B 与 独立 定义:设A,B,C ( ) ( ) ( ) 三个事件,满足P AB P A P B = , P(AC)=P(A)P(C),P BC P B P C P ABC P A P B P C ( ) ( ) ( ) ( ) ( ) ( ) ( ) , = = 及 则称事件A,B,C相互独立. 注:三个事件中的任意两个都相互独立,不可得这三 个事件相互独立

例如:袋中有四个球,其中一个红球、一个白球、一个黑球,还有一个画着红、白、黑三种颜色的球.现从袋中任取一球,并设A,B,C分别表示取出的球上画有红、白、黑各色的事件,则由古典概型的公式计算:P(BC)= P(BC)= P(BA) =P(BA)= P(B)= 0.5P(AB)= P(AB)= P(AC)= P(AC)= P(A)=0.5P(C|A) = P(C|A)= P(C|B)= P(C|B) = P(C) = 0.5这说明事件A,B.C是两两相互独立,于是有P(AB) = P(A)P(B)=0. 25;P (AC) =P (A) P (C) =0. 25P(BC)=P(B)P(C)=0. 25但 P(ABC)=== = P(A)P(B)P(C)48注:定义n个事件的相互独立类似,必须有2"-1-n个式子成立
例如:袋中有四个球,其中一个红球、一个白球、一个 黑球,还有一个画着红、白、黑三种颜色的球.现从袋中 任取一球,并设A,B,C分别表示取出的球上画有红、白、 黑各色的事件,则由古典概型的公式计算: P B C P B C P B A P B A P B ( ) ( ) ( ) ( ) ( ) 0.5 = = = = = P A B P A B P A C P A C P A ( ) ( ) ( ) ( ) ( ) 0.5 = = = = = P C A P C A P C B P C B P C ( ) ( ) ( ) ( ) ( ) 0.5 = = = = = 这说明事件A,B,C是两两相互独立,于是有: ( ) ( ) ( ) 1 1 ( ) ( ) ( ) ( ) 4 8 P AB P A P B P ABC P A P B P C = = = =0.25;P(AC)=P(A)P(C)=0.25 P(BC)=P(B)P(C)=0.25但 注:定义n个事件的相互独立类似,必须有2 n -1- n个式子成立
例1:甲乙各自炮击同一敌机,甲击中的概率时0.7,乙击中的概率为0.8,求敌机被击中的概率解:用A,B分别表示“甲击中敌机”与“乙击中敌机”则敌机被击中的概率:P(AUIB)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)P(B=0. 7+0. 8-0. 56= 0. 94例2:系统有多个元件组成,具所有元件都独立地工作设每个元件正常工作的概率都为p,求以下三种情况下系统正常工作的概率(系统的可靠性)
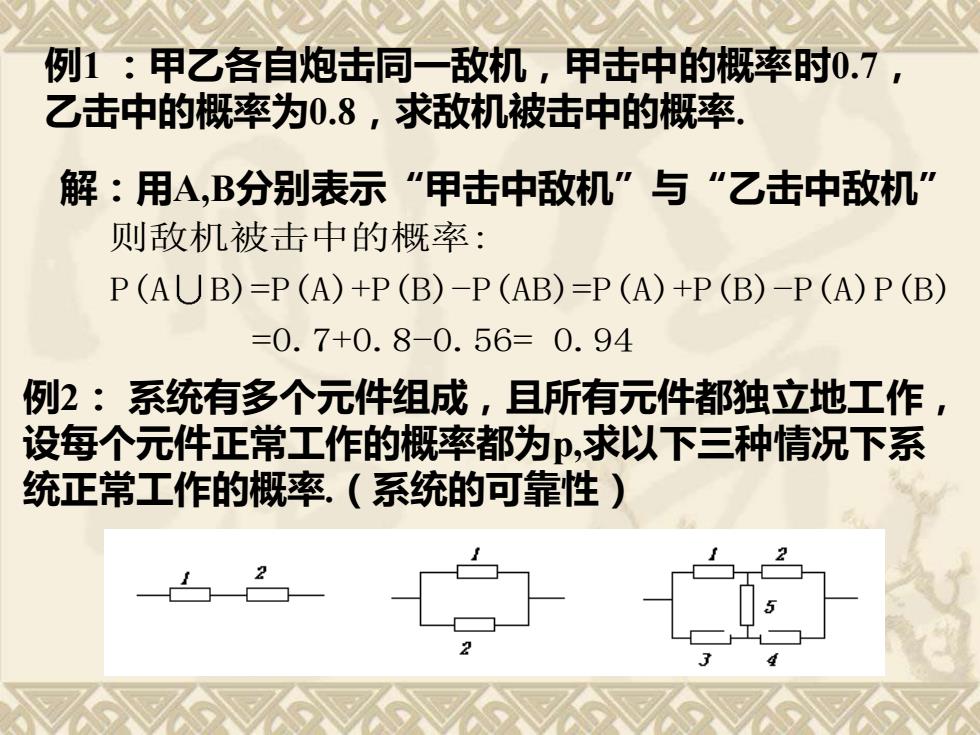
例1 :甲乙各自炮击同一敌机,甲击中的概率时0.7, 乙击中的概率为0.8,求敌机被击中的概率. 解:用A,B分别表示“甲击中敌机”与“乙击中敌机” 则敌机被击中的概率: P(A B)=P(A)+P(B)-P(AB)=P(A)+P(B)-P(A)P(B) =0.7+0.8-0.56= 0.94 例2: 系统有多个元件组成,且所有元件都独立地工作, 设每个元件正常工作的概率都为p,求以下三种情况下系 统正常工作的概率.(系统的可靠性)

解:设S表示第种情况下系统正常工作(i=1,2,3)A表示第k个元件正常工作(k=1,2,3,4,5)(1) P(S)= P(AA)= P(A)P(A)= p(2) P(S2)= P(A U A)= P(A)+ P(A)-P(A)P(A)=2p-p(3) P(S,)= P(A,S,)+ P(A,S,) = P(S, |As)P(As)+ P(S, |A)P(A)P(S3 /A) = P(A U A,)(A, U A)= P(A UA,)P(A, UA)=(P(AUA)) =(2p-p) = p(2-p)P(S: |A)= P(A,A, U A,A)= P(A,A)+ P(A,A4)- P(A,A,A,A4)= 2P(AA)- P(A)4 = 2p2 - p4 = p(2- p)则 : P(S,)= P(S |A,)P(A,)+ P(S A)P(A,=p(2 -p)2 +p2(2-p)(1-p)
i 解:设S i 表示第 种情况下系统正常工作(i=1,2,3) A k k 表示第 个元件正常工作(k=1,2,3,4,5) 2 1 1 2 1 2 (1) ( ) ( ) ( ) ( ) P S P A A P A P A p = = = 2 2 1 2 1 2 1 2 (2) ( ) ( ) ( ) ( ) ( ) ( ) 2 P S P A A P A P A P A P A p p = = + − = − 3 5 3 5 3 3 5 5 3 5 5 (3) ( ) ( ) ( ) ( ) ( ) ( ) ( ) P S P A S P A S P S A P A P S A P A = + = + 3 5 1 3 2 4 1 3 2 4 2 2 2 2 2 1 3 ( ) (( )( )) ( ) ( ) ( ( ) ) (2 ) (2 ) P S A P A A A A P A A P A A P A A p p p p = = = = − = − 3 5 1 2 3 4 1 2 3 4 1 2 3 4 4 2 4 2 2 1 2 1 ( ) ( ) ( ) ( ) ( ) 2 ( ) ( ) 2 (2 ) P S A P A A A A P A A P A A P A A A A P A A P A p p p p = = + − = − = − = − 3 3 5 5 3 5 5 3 2 2 2 : ( ) ( ) ( ) ( ) ( ) (2 ) (2 )(1 ) P S P S A P A P S A P A p p p p p = + = − + − − 则