
3.4 随机变量的独立性利用两个事件相互独立的概念,我们自然引入两个随机变量相互独立的定义:定义1设X,Y是两个随机变量,如果对任意二实数集S,T由(XES)与YeT}构成的可能事件相互独立,则称这两个随机变量是相互独立的,简称是独立的设F(xy)及Fx(x),F)分别是随机变量X与Y的联合分布函数和边缘分布函数.则不难证明,关于两个随机变量相互独立有如下两个等价定理
定义1 设X,Y是两个随机变量, 如果对任意二 实数集S,T, 由 与 构成的可能事件相互 独立, 则称这两个随机变量是相互独立的, 简称是 独立的. 3.4 随机变量的独立性 利用两个事件相互独立的概念, 我们自然引入 两个随机变量相互独立的定义 : 设F(x,y)及FX(x),FY (y)分别是随机变量X与Y 的联合分布函数和边缘分布函数.则不难证明,关 于两个随机变量相互独立有如下两个等价定理. { } X S { } Y T
定理1对二维离散型随机变量,有下面等价关系:在(X,Y)的所有可能取值点x,,J,),有P[X =X,Y = y,}= P(X = x,}P[Y = y,}对任意二实数,y有随机变量X与等价F(x,y)=Fx(x)F(y)Y相互独立在X,Y)的所有可能取值点对任意二实数集S,T:P(Y =y; IX =x,}= P(Y = J,)PXES,YET!P(X=X,IY=y,=P(X=X,)=PXESPYE二
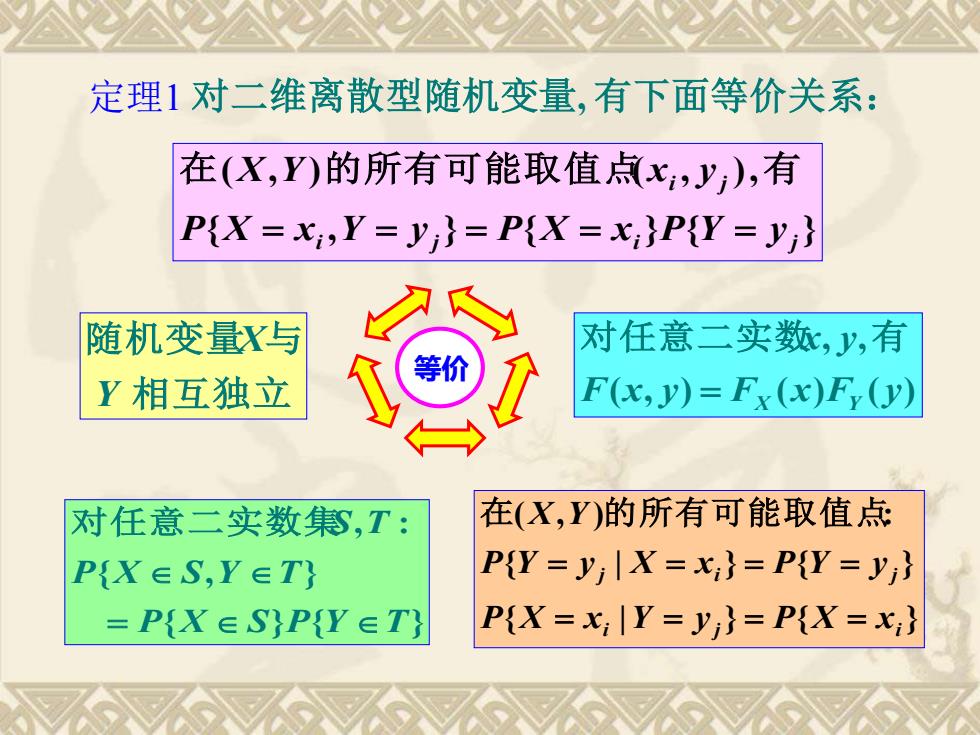
定理1 对二维离散型随机变量, 有下面等价关系: { | } { } { | } { } ( , ) : i j i j i j P X x Y y P X x P Y y X x P Y y X Y = = = = = = = = 在 的所有可能取值点 { , } { } { } ( , ) ( , ), i j i j i j P X x Y y P X x P Y y X Y x y = = = = = 在 的所有可能取值点 有 { } { } { , } , : P X S P Y T P X S Y T S T = 对任意二实数集 ( , ) ( ) ( ) , , F x y F x F y x y = X Y 对任意二实数 有 相互独立 随机变量 与 Y X 等价
定理2对二维连续型随机变量,有下面等价关系:在整个二维平面上有f(x,y)=fx(x)f(y)(几乎)对任意二实数,y有随机变量与等价F(x,y)=Fx(x)F(y)Y相互独立在(X,Y)的所有可能取值点对任意二实数集S,T:fyx(yx)=f(y)(几乎)PXES,YET!fxr(xly)=fx(x)(几乎)=PXESPYEET
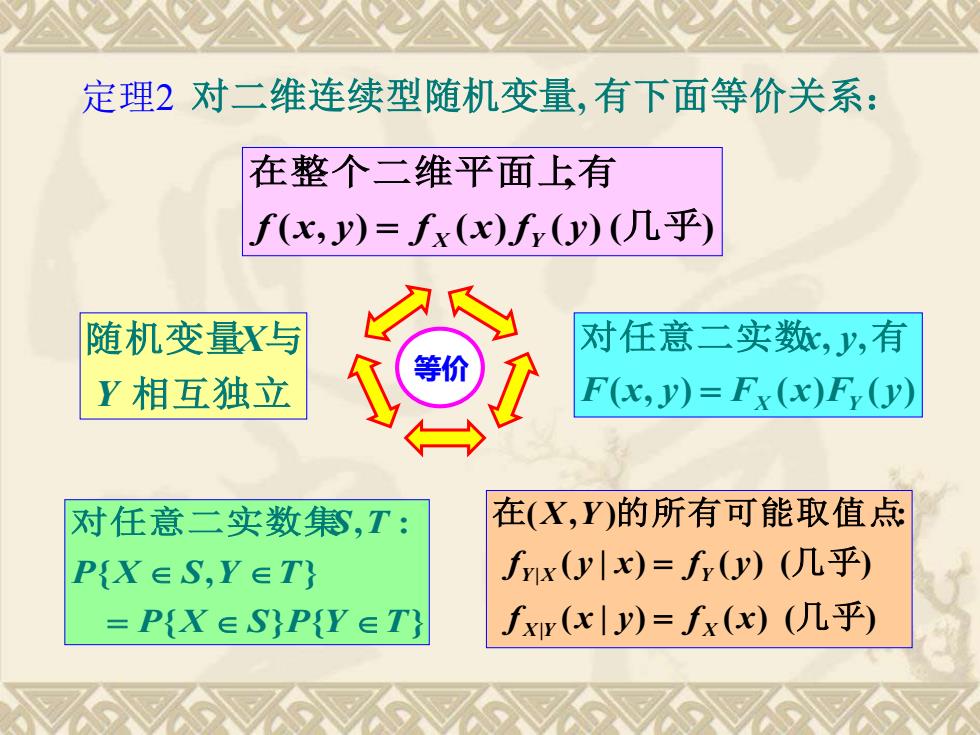
定理2 对二维连续型随机变量, 有下面等价关系: ( | ) ( ) ( ) ( | ) ( ) ( ) ( , ) : | | 几 乎 几 乎 在 的所有可能取值点 f x y f x f y x f y X Y X Y X Y X Y = = ( , ) ( ) ( ) ( ) , 几 乎 在整个二维平面上有 f x y f x f y = X Y { } { } { , } , : P X S P Y T P X S Y T S T = 对任意二实数集 ( , ) ( ) ( ) , , F x y F x F y x y = X Y 对任意二实数 有 相互独立 随机变量 与 Y X 等价
例1在3.1节例1中定义的X与Y是否相互独立?解在3.1节和3.2节已求得Y2314Pi.X001/ 40101/8021/81741/121/121/1231/401/161/161/41/161/1641332571P.j484848487由于 P(X =2)P(Y =3} =P(X = 2,Y = 3} = 0448所以,X与Y不是相互独立的
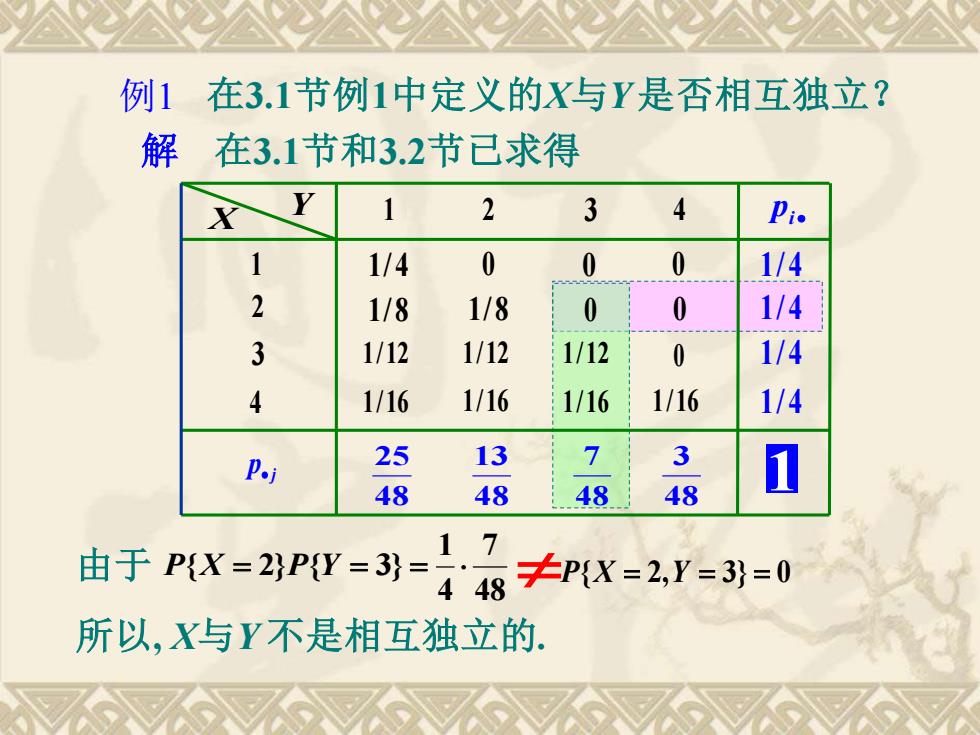
解 例1 在3.1节例1中定义的X与Y是否相互独立? 在3.1节和3.2节已求得 P{X = 2,Y = 3} = 0 48 7 4 1 由于 P{X = 2}P{Y = 3} = 所以, X与Y 不是相互独立的. j 1 p• 48 25 48 13 48 7 48 3 pi • 1/ 4 1/ 4 1/ 4 1/ 4 X Y 1/ 4 1/ 8 1/12 1/16 0 1/ 8 1/12 1/16 0 1/12 1/16 0 0 1/16 1 2 3 4 1 2 3 4 0 0

例2在3.1节例2中定义的X与Y是否相互独立?[2e-(2x+y), x >0,y>0解由3.1节知f(x,y)=其它[0,2e-2xe-", y>0,x>0,1 fx(x)由3.2节知f(y)=0,x≤0,0,y≤0由于对任意的(x,y)(x>0,y>0),都有fx(x)fr(y)=2e-2*e-"= f(x, J)而在其它点,都有fx(x)f,(y)= 0. 0= f(x,y)所以,X与Y是相互独立的
解 例2 由3.1节知 = − + 0, 其它 2e , 0, 0 ( , ) (2 ) x y f x y x y = − 0, 0, 2e , 0, ( ) 2 x x f x x X = − 0, 0 e , 0 ( ) y y f y y 由3.2节知 Y 在3.1节例2中定义的X与Y是否相互独立? 由于对任意的(x, y) (x>0, y>0), 都有 所以, X与Y 是相互独立的. f X (x) f Y ( y) = − x − y 2e e 2 = f (x, y) 而在其它点, 都有 f X (x) f Y ( y) = 00= f (x, y)