
2.3连续型随机变量的概率分布一.连续型随机变量定义:设随机变量X的分布函数F(x),如果存在一个非负可积函数(x),对任意实数x,有F(x) = /m f(x)dx则称这类随机变量X为连续型随机变量。称其中的(x)为X的分布密度或概率密度简称密度。称相应的分布为连续型分布
2.3 连续型随机变量的概率分布 一.连续型随机变量定义: 设随机变量X的分布函数F(x),如果存在一个 非负可积函数f(x),对任意实数x ,有 − = x F(x) f (x)dx 则称这类随机变量X为连续型随机变量。 称相应的分布为连续型分布。 称其中的f(x)为X的分布密度或概率密度, 简称密度

注①:连续型随机变量的分布函数必定连续:分布函数连续的随机变量未必是连续型的随机变量注②:连续型随机变量取任意一点的概率必为零注③:不可能事件的概率为0,概率为0的事件并不一定是不可能事件必然事件的概率为1,概率为1的事件不一定是必然事件
注①:连续型随机变量的分布函数必定连续;分布 函数连续的随机变量未必是连续型的随机变量; 注②:连续型随机变量取任意一点的概率必为零; 注③:不可能事件的概率为0, 概率为0的事件并不一定是不可能事件; 必然事件的概率为1, 概率为1的事件不一定是必然事件

二.连续型随机变量密度函数性质:1°密度函数f(x)在(-o0,+o)上满足f(x) ≥0, f f(x)dx =12°在f(x)的连续点处F(x)可导,且F'(x) = f(x)3°对任意的实数a,b(a<b)都有Pla≤X≤b) =Pa<X<b)=Pia≤X<b= P(a<X≤b)= f" f(x)dx
1 密度函数 f (x) 在(-∞, +∞) 上满足 ( ) 0, ( ) = 1 + − f x f x dx 2 在 f (x) 的连续点处F(x)可导, 且 3 对任意的实数a, b (a<b)都有 F(x) = f (x) = b a f (x)dx P{a X b} = P{a X b} = P{a X b} = P{a X b} 二.连续型随机变量密度函数性质:
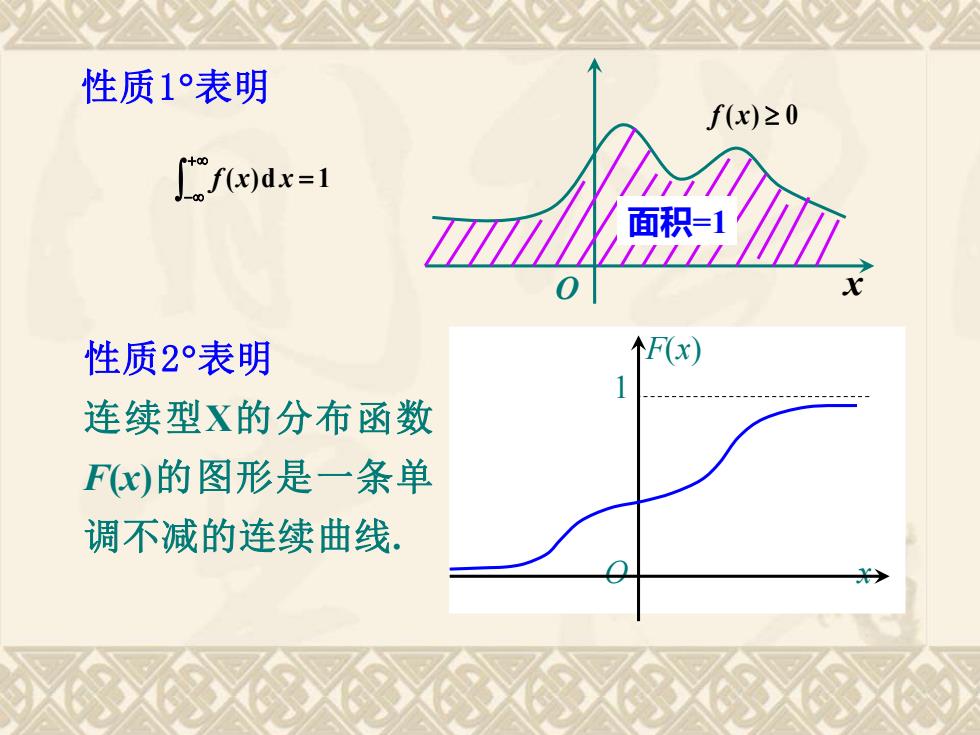
性质1°表明f(x)≥0 f(x)dx=1面积=1T/////o1XF(x)性质2°表明连续型X的分布函数F(x)的图形是一条单调不减的连续曲线
面积=1 O x 性质1表明 性质2表明 连续型X的分布函数 F(x)的图形是一条单 调不减的连续曲线. F(x) 1 O x ( )d = 1 + − f x x f (x) 0
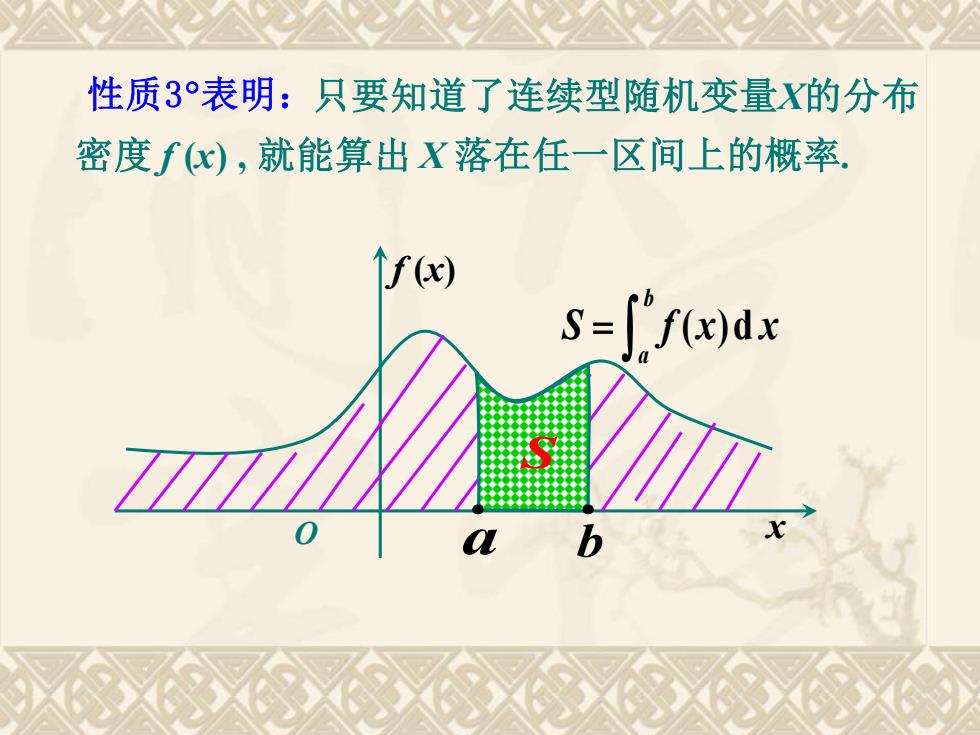
性质3°表明:只要知道了连续型随机变量X的分布密度f(x),就能算出X落在任一区间上的概率f (x)S=f(x)dx1177b
只要知道了连续型随机变量X的分布 密度 f (x) , 就能算出 X 落在任一区间上的概率. S f x x b a ( )d = S a b x f (x) O • • 性质3表明: