第一节向量及其线性运算运算规律交换律a+b=b+a.结合律a+(b+c)=(a+b)+c=a+b+c.运算规律的验证台三角形法则可以推广到多个向量相加的情形S如,s=a+b+c+d+ea返回MathGS公式数学家上页下页线与面
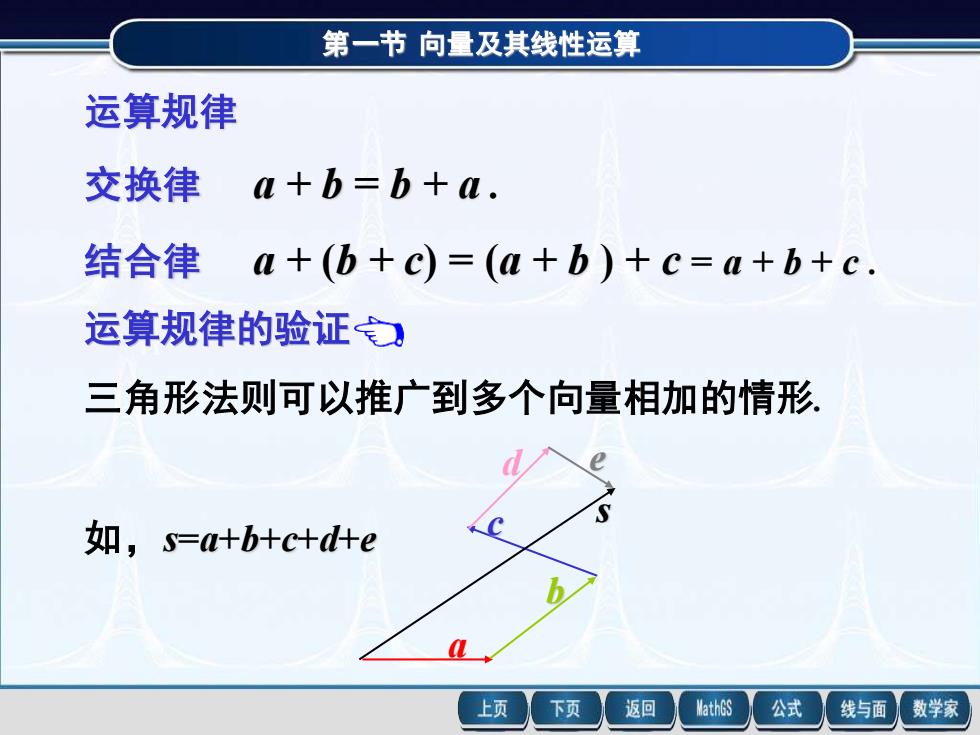
第一节 向量及其线性运算 运算规律 交换律 a + b = b + a . 结合律 a + (b + c) = (a + b ) + c = a + b + c . 第一节 向量及其线性运算 x o y z a a + b b b 求和向量的动态过程 运算规律的验证 三角形法则可以推广到多个向量相加的情形. 如,s=a+b+c+d+e a b c d e s

第一节向量及其线性运算2.向量的减法定义 b-a=b+(-a).显然,对于所有的向量,都有a+0=a,a-a=a+(-a)=0返回MathGS公式上页下页线与面数学家
第一节 向量及其线性运算 2.向量的减法 定义 b – a = b + (– a ). 显然,对于所有的向量 a ,都有 a + 0 = a , a – a = a+ (– a ) = 0

第一节向量及其线性运算3.向量与数的乘法定义设k为一数,向量a与数k的乘积是一个新向量,记作ka。当k>0时,ka与a同向,且lka|=klal当k<0时,ka与a反向,且lka|=-klal当k=0时,ka=0.总之有|ka|=|klla|-2a2aMathGS上页下页返回公式线与面数学家
第一节 向量及其线性运算 3. 向量与数的乘法 定义 设 k 为一数,向量 a 与数 k 的乘积是一个 新向量,记作 ka . 当 k > 0 时,ka 与 a 同向,且 | ka | = k | a | ; 当 k < 0 时,ka 与 a 反向,且 | ka | = -k | a | ; 当 k = 0 时,ka = 0. 总之有 | ka | = | k | | a | . a 2a -2a

第一节向量及其线性运算运算规律结合律(ua) = μu(la) = (au) a ;分配律(a+μ)a=aa+ua,a(a+b)=aa+ab.是一与同向的单位对于非零向量a,向量 e.向量,且a=ale。:这一过程称为把向量a单位化定理1非零向量,b平行的充要条件是,存在实数,使得b=a.证明包上页下页返回MathGS公式数学家线与面
第一节 向量及其线性运算 运算规律 结合律 (a) = (a) = ( ) a ; 分配律 ( + ) a = a + a , (a + b) = a + b . 对于非零向量a,向量 | | . a a = a e 是一与a同向的单位 向量,且 a a ea | | 1 = 这一过程称为把向量a单位化. 定理1非零向量 a , b 平行的充要条件是,存在实数 ,使得 b = a . 第一节 向量及其线性运算 定理1 非零向量 a , b 平行的充要条件是,存在实数 ,使得 b = a . 证明 必要性 设 a 与 b 平行,取 , | | | | a b = 当 a , b 同向时取正,反向时取负.则 b 与 a 同向,且 | | | |. | | | | | | | || | a b a b a = a = = 使得 b = a . 再证唯一性.设又有b = a ,则( - )a = 0, 而 | a | 0 ,故 | - | = 0,即 = .