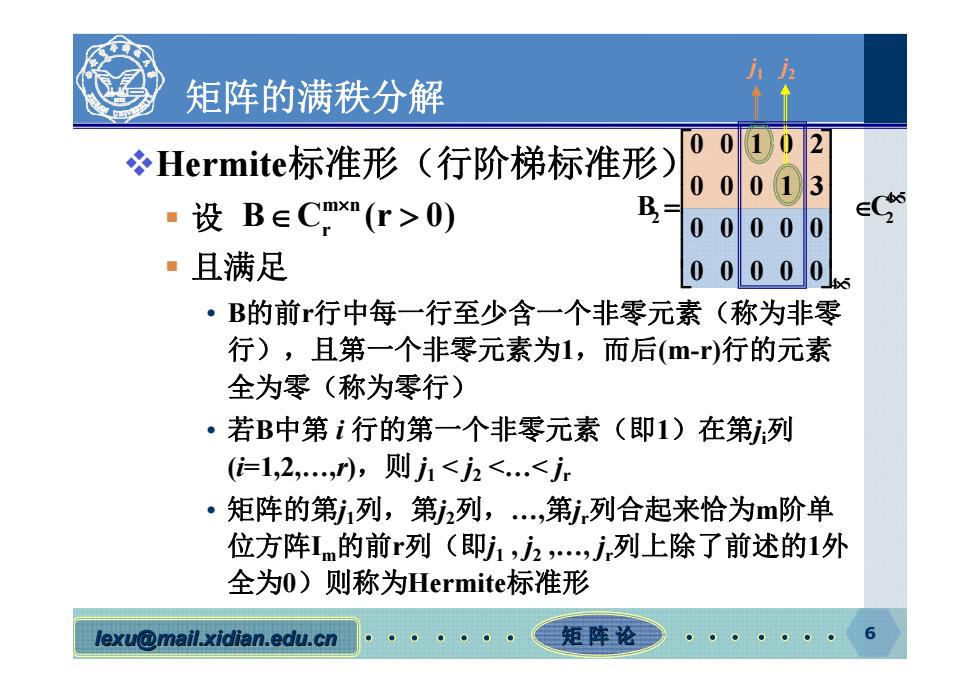
矩阵的满秩分解 Hermite标准形(行阶梯标准形) 00102 0001 3 a设B∈Cmx"(r>0) B 0000 0 ·且满足 00000s ·B的前行中每一行至少含一个非零元素(称为非零 行),且第一个非零元素为1,而后(m-r)行的元素 全为零(称为零行) ·若B中第i行的第一个非零元素(即1)在第j列 (1,2,),则j1<j2<.<j ·矩阵的第j1列,第j2列,,第,列合起来恰为m阶单 位方阵1m的前r列(即j1,j2,,j,列上除了前述的1外 全为0)则称为Hermite标准形 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 矩阵的满秩分解 Hermite标准形(行阶梯标准形) 设 且满足 • B的前r行中每一行至少含一个非零元素(称为非零 行),且第一个非零元素为1,而后(m-r)行的元素 全为零(称为零行) • 若B中第 i 行的第一个非零元素(即1)在第ji列 (i=1,2,…,r),则 j1 < j2 <…< jr • 矩阵的第j1列,第j2列,…,第jr列合起来恰为m阶单 位方阵Im的前r列(即j1 , j2 ,…, jr列上除了前述的1外 全为0)则称为Hermite标准形 m n B C (r 0) r 4 5 2 2 4 5 00102 00013 B C 00000 00000 j1 j2

矩阵的满秩分解 冬满秩分解的一种求法 A=FG ·设A∈Cmxm ·采用行初等变换将A化成Hermite标准形,其矩阵形 式为EA=B,其中B为Hermite标准形定义中给出 的形状 ·选取置换矩阵 一用P右乘任何矩阵(可乘性得到满足时),即可将该矩阵 的第j:列置换到新矩阵(即乘积矩阵)的第1列 令P=[BI] =[ee.…e,]neCw r列(n-r)列 ·令G=B的前r行∈Cr F=AP∈Cmx lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 7 矩阵的满秩分解 满秩分解的一种求法 设 • 采用行初等变换将A化成Hermite标准形,其矩阵形 式为EA=B,其中B为Hermite标准形定义中给出 的形状 • 选取置换矩阵 m n A Cr – 用P右乘任何矩阵(可乘性得到满足时),即可将该矩阵 的第ji列置换到新矩阵(即乘积矩阵)的第i列 – 令 • 令G=B的前r行 1 r (n r) P P |* 列 列 1 2r n r 1 j jj r n r P e e ...e C r n Cr m r F AP C 1 r A FG

第14讲矩阵的奇异值分解 冬酉对角分解 一般矩阵的奇异值分解 lexu@mail.xidian.edu.cn 矩阵论●
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 第14讲 矩阵的奇异值分解 酉对角分解 一般矩阵的奇异值分解

酉对角分解 冬厄米矩阵的谱分解 ·A为厄米矩阵,则存在酉矩阵U 0 UHAU= =Λ 0 入 A=UAUH-∑uu ·将U写成列向量形式 i-l U=[u1u2…u.] lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 酉对角分解 厄米矩阵的谱分解 A为厄米矩阵,则存在酉矩阵U 将U写成列向量形式 1 H 2 n O U AU O U u u ... u 12 n n H H iii i 1 A U U uu