
第八节方程的近似解 一、根的隔离 二、二分法 三、切线法 *四、牛顿迭代分形 上页 下页 返回 MathGS 公式 线与面 数学家
第八节 方程的近似解 一、根的隔离 三、切线法 二、二分法 *四、牛顿迭代分形

第八节方程的近似解 一、根的隔离 求方程的近似解,可分两步来做、 第一步是确定根的大致范围。具体来说,就是确定 一个区间,b1,使方程在该区间上只有唯一根.这一 工作称为根的隔离,区间[α,b]称为根的隔离区间。 若函数f)在[a,b1上连续,f(of(b)<0,且严格 单调,则[a,b1一定是一个隔离区间.求隔离区间的方 法一般用作图法 上页 下页 返回 MathGS 公式 线与面 数学家
第八节 方程的近似解 一、根的隔离 求方程的近似解,可分两步来做. 第一步是确定根的大致范围. 具体来说,就是确定 一个区间 [a , b],使方程在该区间上只有唯一根. 这一 工作称为根的隔离,区间 [a , b] 称为根的隔离区间. 若函数 f (x) 在 [a , b] 上连续,f (a)f (b) < 0,且严格 单调,则[a , b] 一定是一个隔离区间. 求隔离区间的方 法一般用作图法

第八节方程的近似解 直接作出函数y=f心)的图形,从图形中估计出曲 线与x轴交点的大致范围即隔离区间.作图时,有时 也可将方程fx)=0转化成等价方程p)=),分别 作函数y=x)和y=x)的图形,确定这两曲线交点 的大致范围即隔离区间 上页 下页 返回 MathGS 公式 线与面 数学家
第八节 方程的近似解 直接作出函数 y = f (x) 的图形,从图形中估计出曲 线与 x 轴交点的大致范围即隔离区间. 作图时,有时 也可将方程 f (x) = 0 转化成等价方程 (x) = (x),分别 作函数 y = (x) 和 y = (x) 的图形,确定这两曲线交点 的大致范围即隔离区间
第八节方程的近似解 例如,对于方程fx)=x-x-1=0,作图如下: 因为 v(x)x+1 f(1)=-1<0, f(2)=5>0, px)=人3 在(1,2)内f'c)>0, x 所以[1,2]为隔离区间. f)=x3-x-1 上页 下页 返回 MathGS 公式 线与面 数学家
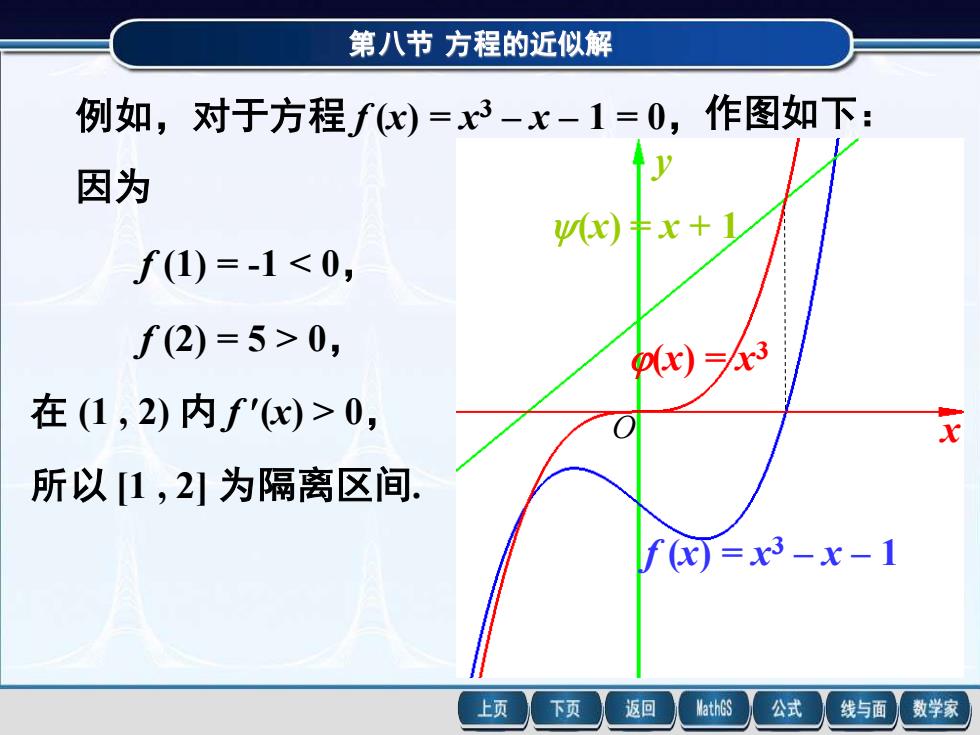
第八节 方程的近似解 例如,对于方程 f (x) = x 3 – x – 1 = 0,作图如下: 因为 f (1) = -1 < 0, f (2) = 5 > 0, 在 (1 , 2) 内 f (x) > 0, 所以 [1 , 2] 为隔离区间. f (x) = x 3 – x – 1 (x) = x 3 (x) = x + 1 x y O

第八节方程的近似解 第二步在隔离区间上求满足精度要求的根.这一步 是求根的关键,主要方法有二分法和切线法. 上页 下页 返回 MathGS 公式 线与面 数学家
第八节 方程的近似解 第二步在隔离区间上求满足精度要求的根. 这一步 是求根的关键,主要方法有二分法和切线法