
第一节微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理 上页 下页 返回 MathS 公式 线与面 数学家
第一节 微分中值定理 一、罗尔定理 二、拉格朗日中值定理 三、柯西中值定理

第一节微分中值定理 一、罗尔定理 1.几何发现 X2 X3( X x 如图所示的曲线,在x1一x6这6个相应点处有水平切 线,这6点均是曲线在局部的最高点或最低点.那么如 何用分析语言来描述这一几何现象呢? 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 微分中值定理 一、罗尔定理 1. 几何发现 如图所示的曲线,在 x1—x6 这6个相应点处有水平切 线,这6点均是曲线在局部的最高点或最低点. 那么如 何用分析语言来描述这一几何现象呢? x1 x2 x3 x4 x5 x6 x y O
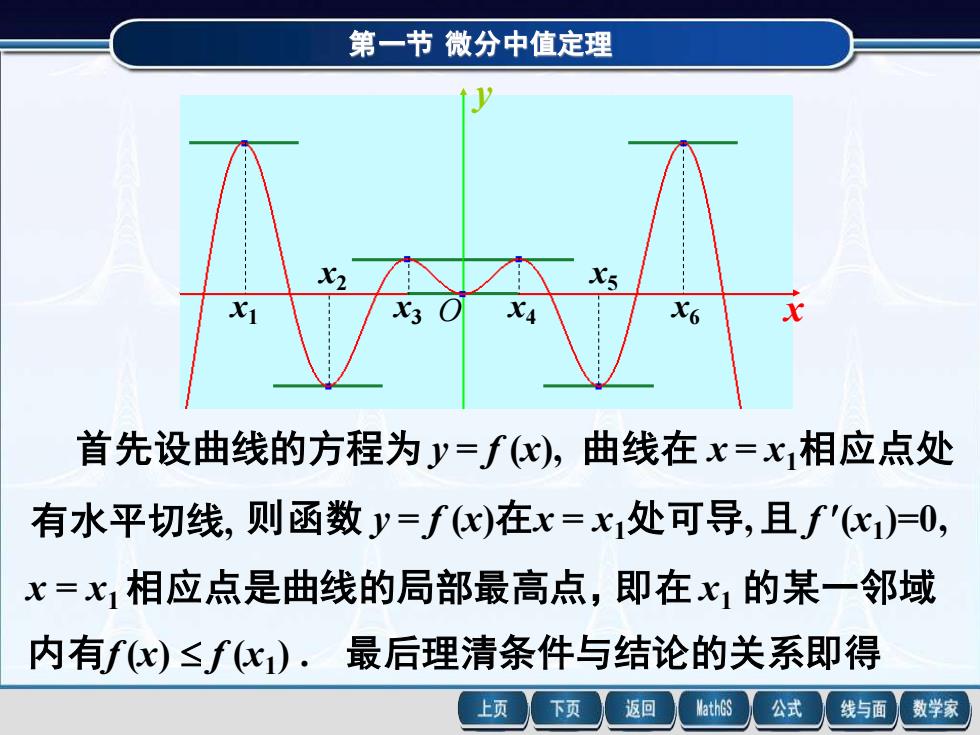
第一节微分中值定理 X> X3( 首先设曲线的方程为y=fx),曲线在x=x相应点处 有水平切线,则函数y=fx)在x=x处可导,且f'比1)=0, x=x相应点是曲线的局部最高点,即在x1的某一邻域 内有fx)≤fc).最后理清条件与结论的关系即得 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 微分中值定理 首先设曲线的方程为 y = f (x), 曲线在 x = x1相应点处 有水平切线, 则函数 y = f (x)在x = x1处可导, 且 f (x1 )=0, x = x1 相应点是曲线的局部最高点,即在 x1 的某一邻域 内有f (x) f (x1 ) . 最后理清条件与结论的关系即得 x1 x2 x3 x4 x5 x6 x y O

第一节微分中值定理 2.费马引理 费马引理设函数fx)在点x的某邻域U心o)内有 定义,并且在xo处可导,如果对任意的x∈Uc),有 fx)≤fco)(或f)≥fc), 那么f')=0. 证明O 通常称导数等于零的点为函数的驻点 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 微分中值定理 2. 费马引理 费马引理 设函数 f (x) 在点 x0 的某邻域 U(x0 ) 内有 定义,并且在 x0 处可导,如果对任意的 x U(x0 ),有 f (x) f (x0 ) (或 f (x) f (x0 )), 那么 f (x0 ) = 0 . 第一节 微分中值定理 证明 费马引理 设函数 f (x) 在点 x0 的某邻域 U(x0 ) 内有 定义,并且在 x0 处可导,如果对任意的 x U(x0 ),有 f (x) f (x0 ) (或 f (x) f (x0 )), 那么 f (x0 ) = 0 . 不妨设 x U(x0 ) 时,f (x) f (x0 ), 则在该邻 内恒有 f (x) – f (x0 ) 0 . f (x0 ) = 0 f (x0 ) 0 且 f (x0 ) 0 下面用左右导数来证明. 通常称导数等于零的点为函数的驻点

第一节微分中值定理 3.罗尔定理 费马引理的结论非常好,但不太好用.有时需要快 速地判别一条曲线在一个指定的区间上是否有水平切线 用费马引理就是要判别曲线是否有局部最高(低)点,且 函数在这点是否可导,而这有时是困难的.因此我们希 望将费马定理的条件进行改造,使之更好用.那么如何 改造呢?我们还是从几何上来找线索 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 微分中值定理 3. 罗尔定理 费马引理的结论非常好,但不太好用. 有时需要快 速地判别一条曲线在一个指定的区间上是否有水平切线 用费马引理就是要判别曲线是否有局部最高(低)点,且 函数在这点是否可导,而这有时是困难的.因此我们希 望将费马定理的条件进行改造,使之更好用. 那么如何 改造呢?我们还是从几何上来找线索