
第三节函数的极限 函数极限的定义 二、函数极限的性质 上页 下页 返回 MathS 公式 线与面 数学家
第三节 函数的极限 一、函数极限的定义 二、函数极限的性质

第三节函数的极限 函数极限的定义 在上一节我们讨论了数列的极限,而数列xm=f() 可以看成是函数y=fx)当自变量x取正整数的特殊情 形.所以,可以用研究数列极限完全相同的思想和方法 来研究函数在自变量的某一变化过程中,函数值的变化 情况,即函数的极限.自变量的变化过程主要有两种: ()自变量趋于有限值(cx): (2)自变量趋于无穷大(x-→∞) 上页 下页 返回 MathGS 公式 线与面 数学家
第三节 函数的极限 一、函数极限的定义 在上一节我们讨论了数列的极限,而数列 xn = f (n) 可以看成是函数 y = f (x) 当自变量x 取正整数的特殊情 形. 所以,可以用研究数列极限完全相同的思想和方法 来研究函数在自变量的某一变化过程中,函数值的变化 情况,即函数的极限. 自变量的变化过程主要有两种: (1) 自变量趋于有限值(x→x0 ); (2) 自变量趋于无穷大(x→)
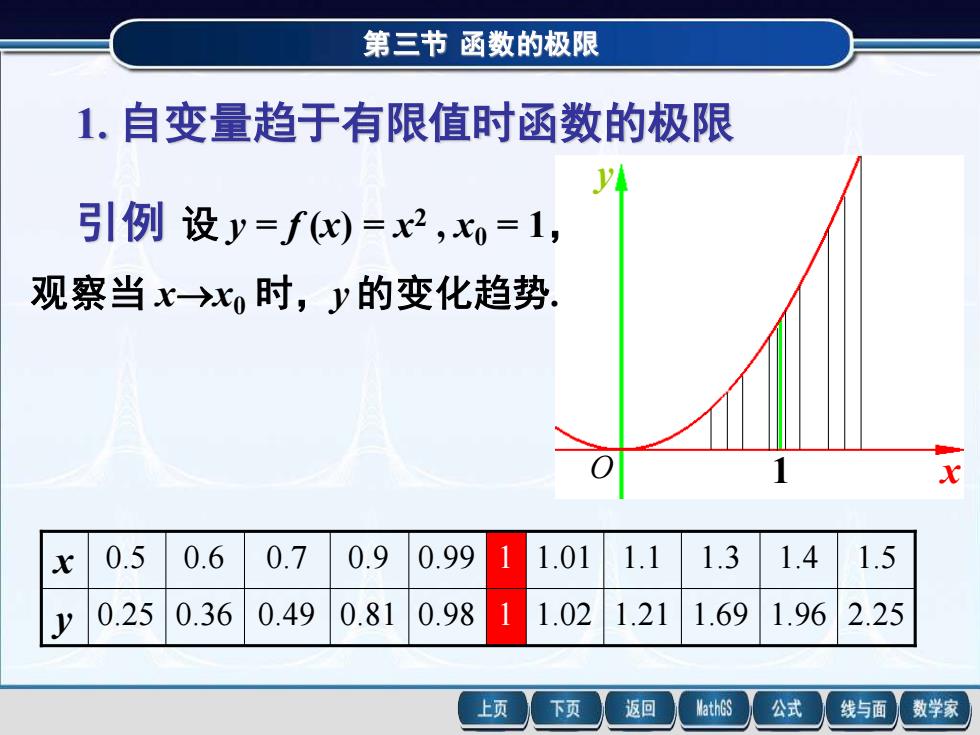
第三节函数的极限 1.自变量趋于有限值时函数的极限 引例设y=fc)=x2,x=1, 观察当xx时,y的变化趋势. 0.5 0.6 0.7 0.9 0.99 1 1.01 1.1 1.3 1.4 1.5 0.25 0.36 0.49 0.81 0.98 1.02 1.21 1.69 1.96 2.25 上页 下页 返回 MathGS 公式 线与面 数学家
第三节 函数的极限 1. 自变量趋于有限值时函数的极限 x y O 1 1.96 1.4 y 0.25 0.36 0.49 0.81 0.98 1 1.02 1.21 1.69 2.25 x 0.5 0.6 0.7 0.9 0.99 1 1.01 1.1 1.3 1.5 引例 设 y = f (x) = x 2 , x0 = 1, 观察当 x→x0 时,y 的变化趋势
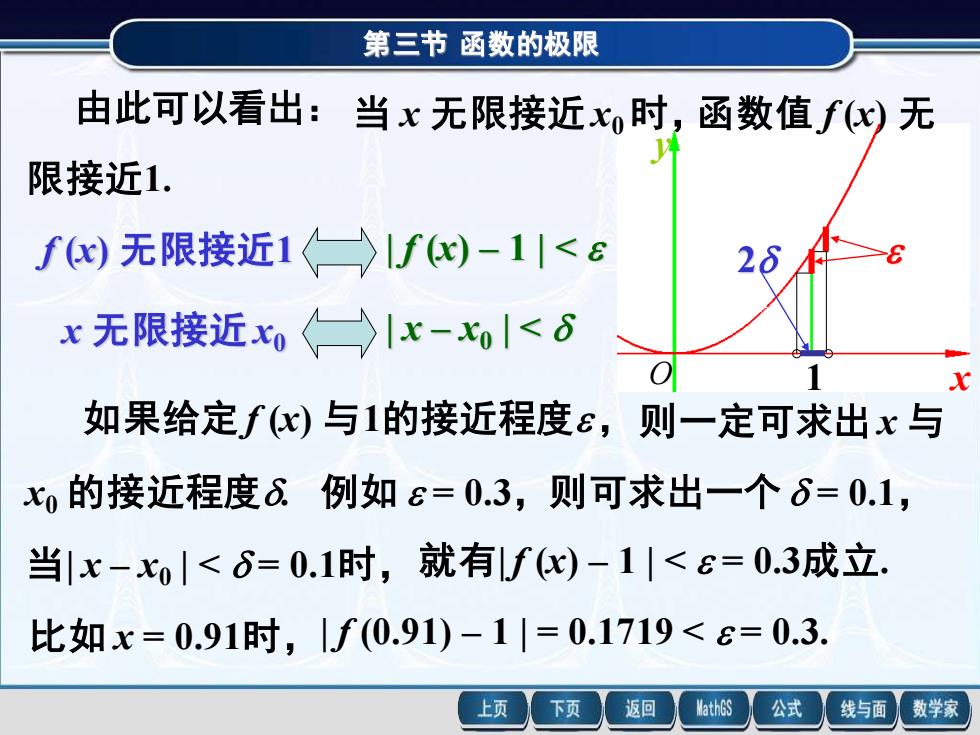
第三节函数的极限 由此可以看出:当x无限接近xo时,函数值fx)无 限接近1. fc)无限接近1)f)-1|< x无限接近xIx-|<6 如果给定fx)与1的接近程度ε,则一定可求出x与 o的接近程度6.例如£=0.3,则可求出一个6=0.1, 当|x-x|<6=0.1时,就有fc)-1<e=0.3成立. 比如x=0.91时,1f(0.91)-1|=0.1719<8=0.3. 上页 下页 返回 MathGS 公式 线与面 数学家
第三节 函数的极限 则一定可求出 x 与 x y O 1 2 由此可以看出: 当 x 无限接近 x0 时,函数值 f (x) 无 限接近1. f (x) 无限接近1 | f (x) – 1 | < x 无限接近 x0 | x – x0 | < 如果给定 f (x) 与1的接近程度, x0 的接近程度. 例如 = 0.3,则可求出一个 = 0.1, 当| x – x0 | < = 0.1时,就有| f (x) – 1 | < = 0.3成立. 比如 x = 0.91时,| f (0.91) – 1 | = 0.1719 < = 0.3. 则一定可求出 x 与

第三节函数的极限 定义1设函数f)在点的某一去心邻域内有定 义.如果存在常数A,对于任意给定的正数ε(不论它 多么小),总存在正数δ,使得当x满足不等式 0<|x-xo|<6 时,对应的函数值f)都满足不等式 1f)-A|<6, 那么常数A就叫做函数fc)当x→x时的极限,记作 lim(x)=A或f)→A(当x→x). x→x0 上页 下页 返回 MathGS 公式 线与面 数学家
第三节 函数的极限 定义1 设函数 f (x) 在点 x0 的某一去心邻域内有定 义.如果存在常数 A,对于任意给定的正数 (不论它 多么小),总存在正数 ,使得当 x 满足不等式 0 < | x – x0 | < 时,对应的函数值 f (x) 都满足不等式 | f (x) – A | < , 那么常数 A 就叫做函数 f (x) 当 x → x0 时的极限,记作 f x A x x = → ( ) lim 0 或 f (x) → A (当 x → x0 )