
第八节方程的近似解 二、二分法 设[,b]是方程f(x)=0根的一个隔离区间,求方 程在该区间内的根。 二分法的基本思想是:用中点把区间[,b]分成两 个子区间,则根必在这两个子区间中的某一个之内, 确定含根的子区间,并以该子区间为新的隔离区间,重 复应用上述步骤,直到求出满足精度要求的根. 二分法的步骤如下: 上页 下页 返回 MathGS 公式 线与面 数学家
第八节 方程的近似解 二、二分法 设 [a , b] 是方程 f (x) = 0 根的一个隔离区间,求方 程在该区间内的根. 二分法的基本思想是:用中点把区间 [a , b] 分成两 个子区间,则根必在这两个子区间中的某一个之内, 确定含根的子区间,并以该子区间为新的隔离区间,重 复应用上述步骤,直到求出满足精度要求的根. 二分法的步骤如下:

第八节方程的近似解 Step1令L=a,R=b,设定求根精度Eps; Step2求中点M=(L+R)/2,若|f(M0l<Eps, 则 x=M即是满足要求的根,求根结束.否则转Step3; Step3若f(Lf0<0,则令L=a,R=M转Step2, 若fMf(R)<0,则令L=M,R=b转Step2. f(Lf(M)<0 M R x Mf(M)f(R)<0 元 M R L R x LR 文 上页 下页 返回 MathGS 公式 线与面 数学家
第八节 方程的近似解 Step1 令 L = a , R = b , 设定求根精度 Eps; Step2 求中点 M = (L + R)/2 , 若 | f (M)| < Eps, 则 x = M 即是满足要求的根,求根结束. 否则转Step3; Step3 若 f (L)f (M) < 0,则令 L = a , R = M 转Step2, 若 f (M)f (R) < 0,则令 L = M , R = b 转Step2. L R f (L)f (M) < 0 M x L R M f (M)f (R) < 0 x L R M x L R x
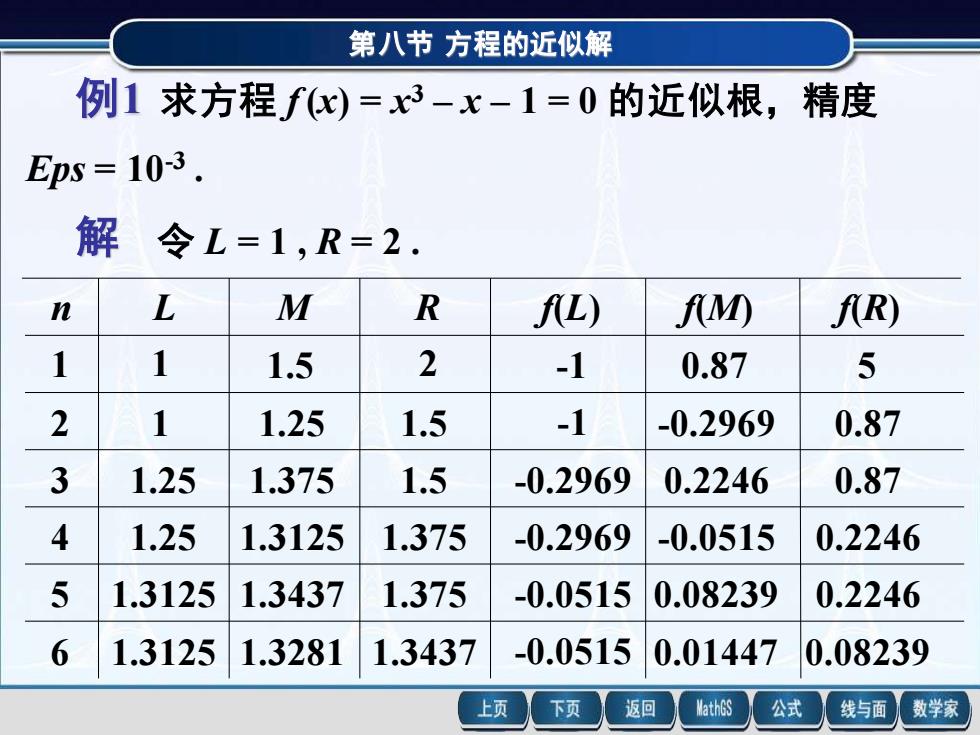
第八节方程的近似解 例1求方程fx)=x3-x-1=0的近似根,精度 Eps=10-3. 解 令L=1,R=2. n L M R AL fM) AR) 1 1 1.5 2 -1 0.87 5 2 1 1.25 1.5 -1 -0.2969 0.87 3 1.25 1.375 1.5 -0.2969 0.2246 0.87 4 1.25 1.3125 1.375 -0.2969 -0.0515 0.2246 5 1.3125 1.3437 1.375 -0.0515 0.08239 0.2246 6 1.3125 1.3281 1.3437 -0.0515 0.01447 0.08239 上页 下页 返回 MathGS 公式 线与面 数学家
第八节 方程的近似解 例1 求方程 f (x) = x 3 – x – 1 = 0 的近似根,精度 Eps = 10-3 . 解 令 L = 1 , R = 2 . L M R f(L) f(M) f(R) 1 1.5 2 -1 0.87 5 n 1 2 1 1.25 1.5 -1 -0.2969 0.87 3 1.25 1.375 1.5 -0.2969 0.2246 0.87 4 1.25 1.3125 1.375 -0.2969 -0.0515 0.2246 5 1.3125 1.3437 1.375 -0.0515 0.08239 0.2246 6 1.3125 1.3281 1.3437 -0.0515 0.01447 0.08239
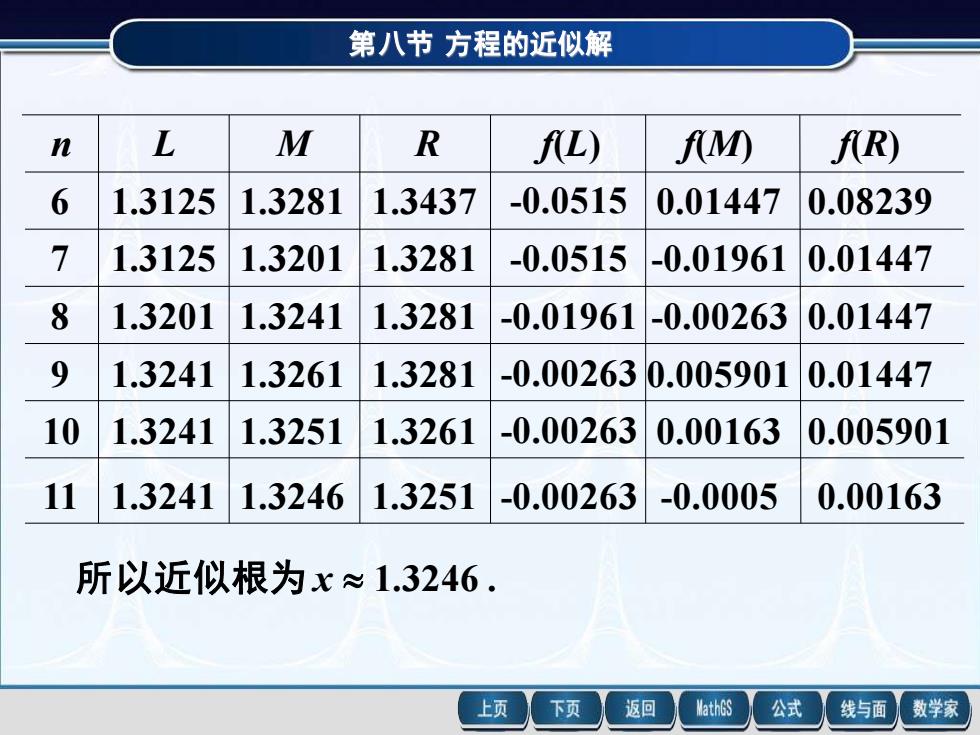
第八节方程的近似解 n L M R fL) fM) AR) 6 1.3125 1.3281 1.3437 -0.0515 0.01447 0.08239 7 1.3125 1.3201 1.3281 -0.0515 -0.01961 0.01447 8 1.3201 1.3241 1.3281 -0.01961 -0.00263 0.01447 9 1.3241 1.3261 1.3281 -0.002630.005901 0.01447 10 1.3241 1.3251 1.3261 -0.00263 0.00163 0.005901 11 1.3241 1.3246 1.3251 -0.00263 -0.0005 0.00163 所以近似根为x≈1.3246. 上页 下页 返回 MathGS 公式 线与面 数学家
第八节 方程的近似解 n L M R f(L) f(M) f(R) 6 1.3125 1.3281 1.3437 -0.0515 0.01447 0.08239 7 1.3125 1.3201 1.3281 -0.0515 -0.01961 0.01447 8 1.3201 1.3241 1.3281 -0.01961 -0.00263 0.01447 9 1.3241 1.3261 1.3281 -0.00263 0.005901 0.01447 10 1.3241 1.3251 1.3261 -0.00263 0.00163 0.005901 所以近似根为 x 1.3246 . 11 1.3241 1.3246 1.3251 -0.00263 -0.0005 0.00163