第一节映射与函数 一、集合 二、映射 三、函数 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 映射与函数 二、映射 三、函数 第一节 映射与函数 合 M , 记作 元素 a 不属于集合 M , 记作 1. 集合的概念 定义 具有某种特定性质的事物的总体称为集合, 组成集合的事物称为元素,不含任何元素的集合称为 空集,记作 , 一、集合 aM , aM. 含有有限个元素的集合称为有限集, 含有无穷多个元素的集合称为无限集.元素 a 属于集

第一节映射与函数 二、映射 1.映射的概念 定义设X,Y是两个非空集合,若存在一个对应 规则f,使得Vx∈X,有唯一确定的y∈Y与之对应, 则称f为从X到Y的映射,记作f:X→Y. X 上页 下页 返回 MathS 公式 线与面 数学家
第一节 映射与函数 1. 映射的概念 二、映射 定义 设 X , Y 是两个非空集合, 若存在一个对应 规则 f , 使得 有唯一确定的 与之对应, 则称 f 为从 X 到 Y 的映射, 记作 f : X → Y . x X , y Y X f Y

第一节映射与函数 元素y称为元素x在映射f下的像,记作y=f(x) 元素x称为元素y在映射f下的原像.集合X称为映 射f的定义域;Y的子集Rr=f(X)={f(xx∈X} 称为∫的值域 注意 ()映射的三要素一定义域,对应规则,值域: (2)元素x的像y是唯一的,但y的原像不一定唯一 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 映射与函数 元素 y 称为元素x 在映射 f 下的像, 记作 y = f ( x). 元素 x 称为元素 y 在映射 f 下的原像. 射 f 的定义域; Y 的子集 Rf = f (X ) = f (x) x X 称为 f 的值域 . 注意 (1) 映射的三要素— 定义域 , 对应规则, 值域. (2) 元素 x 的像 y 是唯一的, 但 y 的原像不一定唯一. 集合 X 称为映
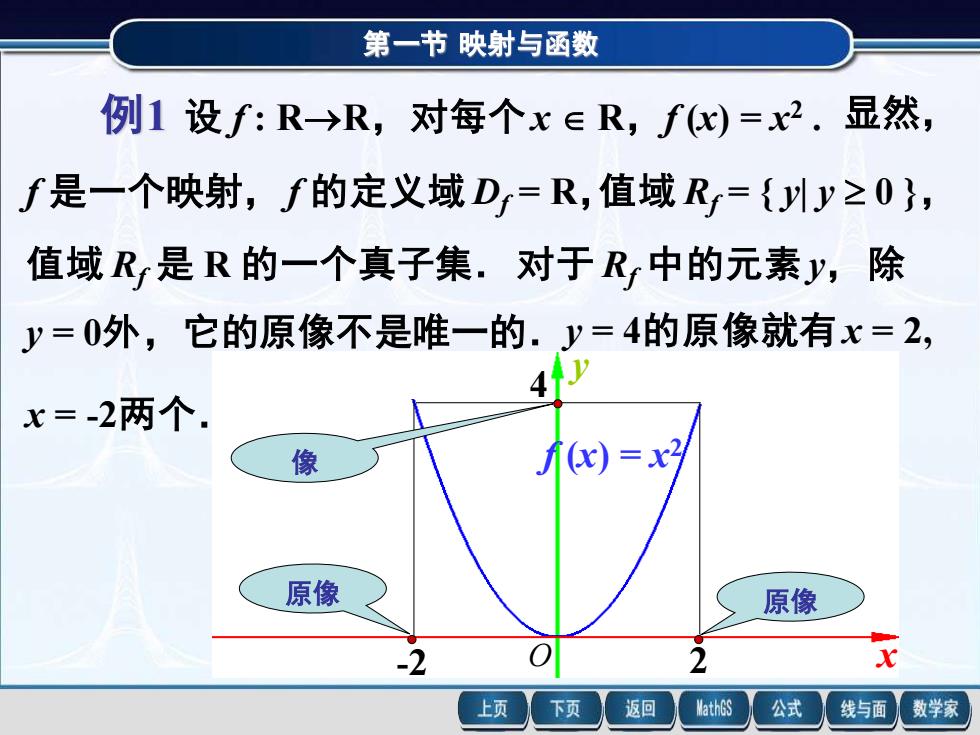
第一节映射与函数 例1设f:R→R,对每个x∈R,fx)=x2.显然, f是一个映射,f的定义域D=R,值域Rr={以y20}, 值域R是R的一个真子集.对于R中的元素y,除 y=0外,它的原像不是唯一的.y=4的原像就有x=2, A x=-2两个. 像 (x) =x 原像 原像 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 映射与函数 x y f (x) = x 2 -2 2 4 原像 原像 像 O 例1 设 f : R→R,对每个x R,f (x) = x 2 . f 是一个映射, f 的定义域 Df = R, 显然, 值域 Rf = { y| y 0 }, 值域 Rf 是 R 的一个真子集.对于 Rf 中的元素 y,除 y = 0外,它的原像不是唯一的.y = 4的原像就有 x = 2, x = -2两个.

第一节映射与函数 例2设X={化,y)|x2+y2=1},Y={c,0)川x≤1, f:X→Y,则对每个x,y)∈X,有唯一确定的c,0)∈Y 与之对应.显然f是一个映射,定义域D=X,,值域 R=Y.在几何上,这个映射表示将平面上一个圆心在 原点的单位圆上的点投影到x轴上的区间[-1,1]上. x,) (x,-y) 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 映射与函数 例2 设 X = {(x , y) | x 2 + y 2 = 1},Y = {(x , 0) | |x| 1 }, 与之对应. f : X→Y,则对每个 (x , y) X,有唯一确定的(x , 0) Y 显然f 是一个映射,定义域 Df = X ,值域 Rf = Y .在几何上,这个映射表示将平面上一个圆心在 原点的单位圆上的点投影到 x 轴上的区间 [ -1 , 1 ]上. 1 1 (x , y) x (x , -y) x y -1 -1 O