
第六节函数图形的描绘 一、渐近线 二、绘图步骤 三、举例 上页 下页 返回 MathGS 公式 线与面 数学家
第六节 函数图形的描绘 一、渐近线 三、举例 二、绘图步骤
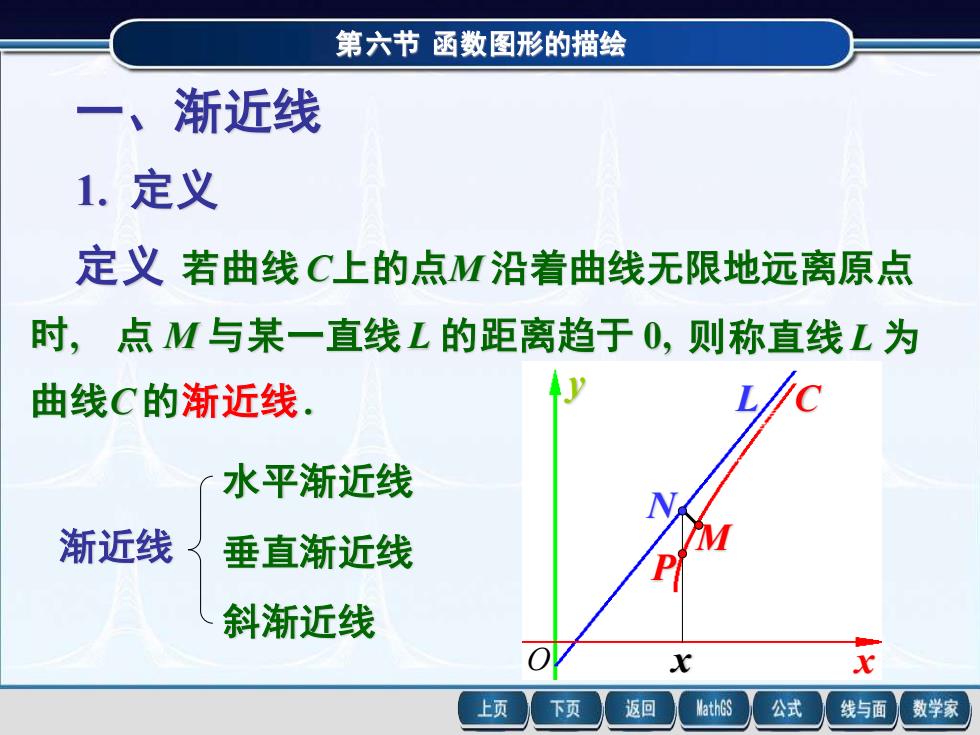
第六节函数图形的描绘 一、渐近线 1.定义 定义若曲线C上的点M沿着曲线无限地远离原点 时,点M与某一直线L的距离趋于0,则称直线L为 曲线C的渐近线. 水平渐近线 渐近线 垂直渐近线 M P 斜渐近线 上页 下页 返回 MathGS 公式 线与面 数学家
第六节 函数图形的描绘 一、渐近线 点 M 与某一直线 L 的距离趋于 0, 定义 若曲线 C上的点M 沿着曲线无限地远离原点 时, 则称直线 L 为 曲线C 的渐近线. 1. 定义 渐近线 水平渐近线 垂直渐近线 斜渐近线 M L C N P x x y O
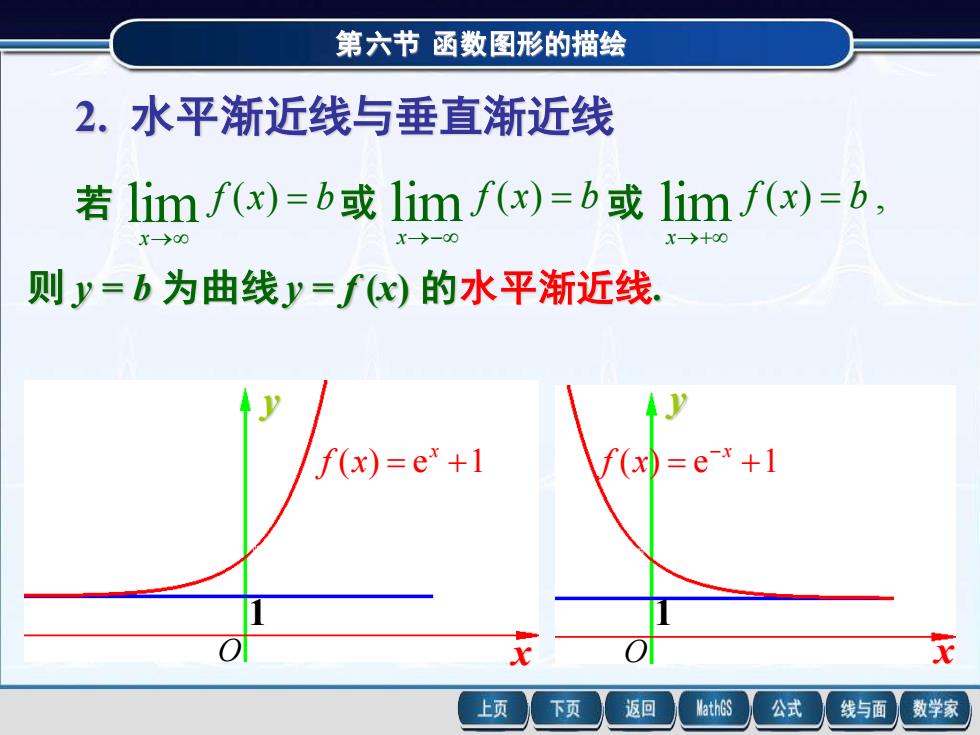
第六节函数图形的描绘 2.水平渐近线与垂直渐近线 若1imf(x)=b或limf(x)=b或limf(x)=b, X-00 X>+00 则y=b为曲线y=fx)的水平渐近线 f(x)=e"+1 f(x)=e *+1 x 上页 下页 返回 MathGS 公式 线与面 数学家
第六节 函数图形的描绘 2. 水平渐近线与垂直渐近线 若 f x b x = → ( ) lim 或 f x b x = →− ( ) lim 或 ( ) , lim f x b x = →+ 则 y = b 为曲线 y = f (x) 的水平渐近线. ( ) = e +1 x f x 1 y O x ( ) = e +1 −x f x 1 y O x
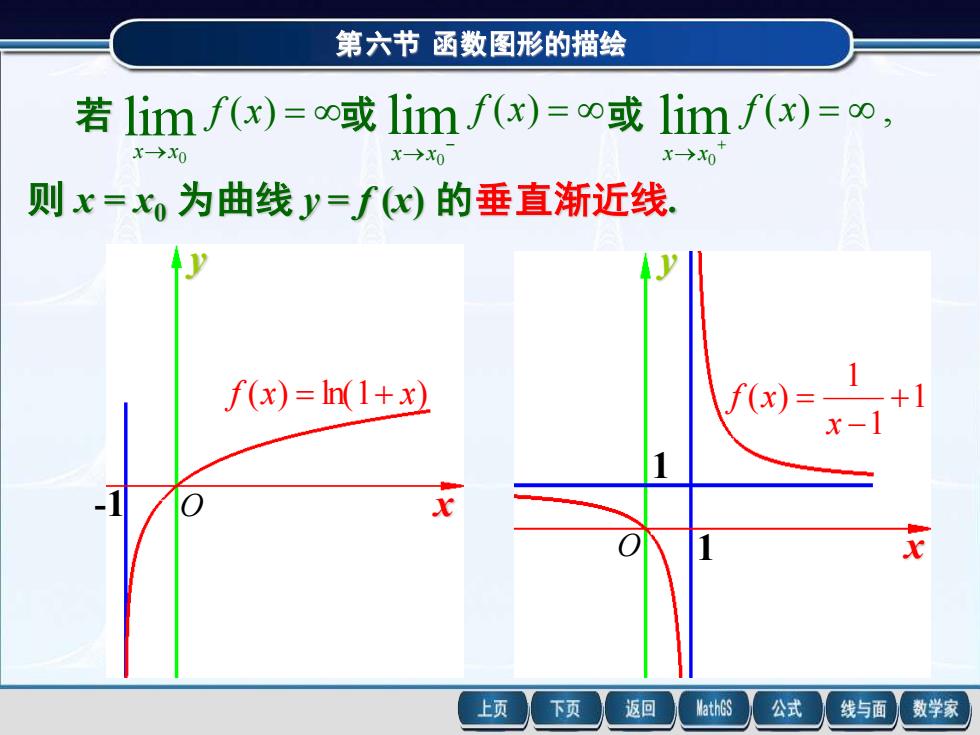
第六节函数图形的描绘 若limf(x)=oo或limf(x)=o或limf(x)=o, x→x0 则x=xo为曲线y=f(心)的垂直渐近线 f(x)=In(1+x) f(x) x-1 上页 下页 返回 MathGS 公式 线与面 数学家
第六节 函数图形的描绘 若 = → ( ) lim 0 f x x x 或 = → − ( ) lim 0 f x x x 或 ( ) , lim 0 = → + f x x x 则 x = x0 为曲线 y = f (x) 的垂直渐近线. f (x) = ln(1+ x) -1 y O x 1 1 1 ( ) + − = x f x y 1 x 1 O

第六节函数图形的描绘 3.斜渐近线 设曲线C的方程为y=f(x), 直线L的方程为y=ax+b(a≠O) 则直线L是曲线C的斜渐近线的 的充要条件为 lim MN =0lim NP=0lim[f(x)-(ax+)]=0 X>00 X→00 →=lm型,-lml-m x->00 上页 下页 返回 MathGS 公式 线与面 数学家
第六节 函数图形的描绘 3. 斜渐近线 设曲线 C 的方程为 y = f (x) , 直线 L 的方程为 y = ax +b (a 0). 则直线 L 是曲线 C 的斜渐近线的 的充要条件为 0 lim = → MN x 0 lim = → NP x [ ( ) ( )] 0 lim − + = → f x ax b x , ( ) lim x f x a x→ = [ ( ) ]. b lim f x ax x = − → M L C N P x x y O