
第一节导数的概念 一、引例 二、导数的定义 三、导数的几何意义 四、可导与连续的关系 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 导数的概念 一、引例 二、导数的定义 三、导数的几何意义 四、可导与连续的关系

第一节导数的概念 一、引例 引例1直线运动的速度 对于匀速直线运动有 经过的路程 平均速度= 所花的时间 其特点是:任一时刻的瞬时速度都相等,且等于任一时 间间隔上的平均速度, 上述公式也可用来求变速直线运动在某一时间间隔上 的平均速度. 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 导数的概念 一、引例 引例1直线运动的速度 对于匀速直线运动有 平均速度 = 经过的路程 所花的时间 其特点是:任一时刻的瞬时速度都相等,且等于任一时 上述公式也可用来求变速直线运动在某一时间间隔上 的平均速度. 间间隔上的平均速度
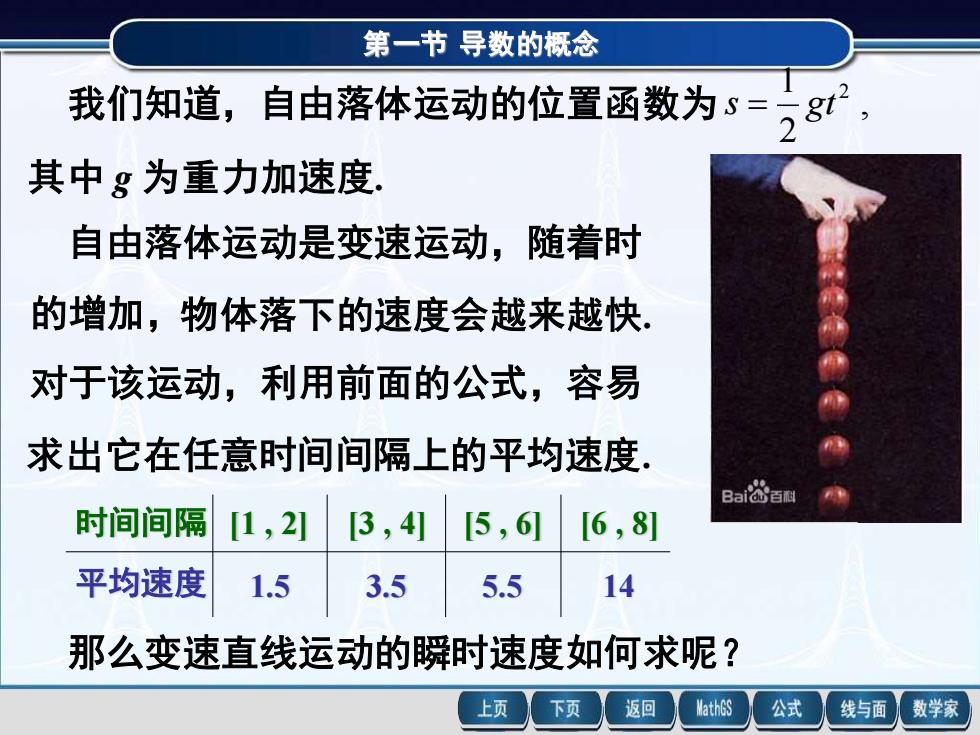
第一节导数的概念 我们知道,自由落体运动的位置函数为5=28, 其中g为重力加速度, 自由落体运动是变速运动,随着时 的增加,物体落下的速度会越来越快, 对于该运动,利用前面的公式,容易 求出它在任意时间间隔上的平均速度 Bai&a国 时间间隔 1,2 [3,4 [5,6 [6,81 平均速度 1.5 3.5 5.5 14 那么变速直线运动的瞬时速度如何求呢? 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 导数的概念 我们知道,自由落体运动的位置函数为 , 2 1 2 s = gt 其中 g 为重力加速度. 自由落体运动是变速运动,随着时 的增加,物体落下的速度会越来越快. 对于该运动,利用前面的公式,容易 求出它在任意时间间隔上的平均速度. 时间间隔 平均速度 [1 , 2] [3 , 4] [5 , 6] 1.5 3.5 5.5 [6 , 8] 14 那么变速直线运动的瞬时速度如何求呢?

第一节导数的概念 设一动点作变速直线运动,其位置函数为s=s), 现在来求它在时刻t的瞬时速度, 为此,在6处取一时间间隔△,于是终止时刻为 t=to+△t. △t=t-t to 则动点在时间间隔△上的平均速度为 s(t)-s(to) t-to 由此可得瞬时速度为 v=lim s(t)-s(to) t→t0 t-to 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 导数的概念 设一动点作变速直线运动,其位置函数为 s = s(t), 现在来求它在时刻 t0 的瞬时速度. 为此,在 t0 处取一时间间隔 t,于是终止时刻为 t0 t t t = t – t0 则动点在时间间隔 t 上的平均速度为 . ( ) ( ) 0 0 t t s t s t v − − = 由此可得瞬时速度为 . ( ) ( ) 0 0 lim 0 t t s t s t v t t − − = → t = t0 + t
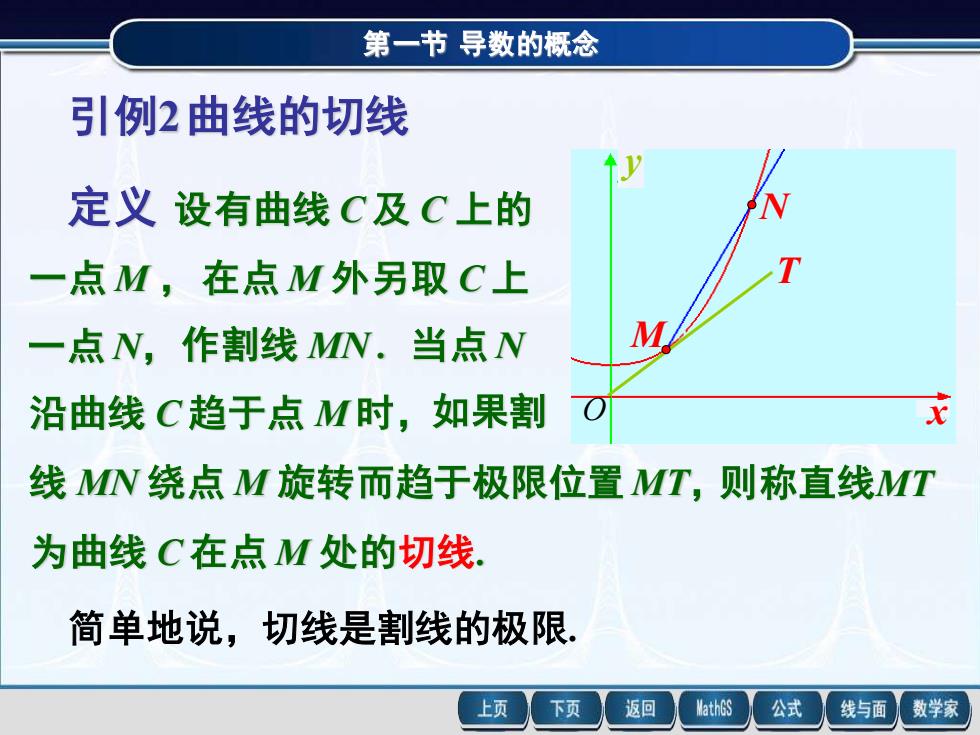
第一节导数的概念 引例2曲线的切线 定义设有曲线C及C上的 一点M,在点M外另取C上 一点N,作割线MN.当点N M 沿曲线C趋于点M时,如果割 线MN绕点M旋转而趋于极限位置MT,则称直线MT 为曲线C在点M处的切线 简单地说,切线是割线的极限 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 导数的概念 引例2曲线的切线 定义 设有曲线 C 及 C 上的 一点 M ,在点 M 外另取 C 上 一点 N,作割线 MN . 当点 N 沿曲线 C 趋于点 M 时,如果割 线 MN 绕点 M 旋转而趋于极限位置 MT,则称直线MT 为曲线 C 在点 M 处的切线. 简单地说,切线是割线的极限. M N T x y O