《高等数学》课程教学资源（PPT课件）第三章微分中值定理与导数的应用_第七节曲率

第七节曲率 一、弧微分 二、曲率及其计算公式 三、曲率圆与曲率半径 四、曲率中心渐屈线与渐伸线 上页 下页 返回 MathS 公式 线与面 数学家

第七节 曲率 一、弧微分 三、曲率圆与曲率半径 二、曲率及其计算公式 *四、曲率中心渐屈线与渐伸线

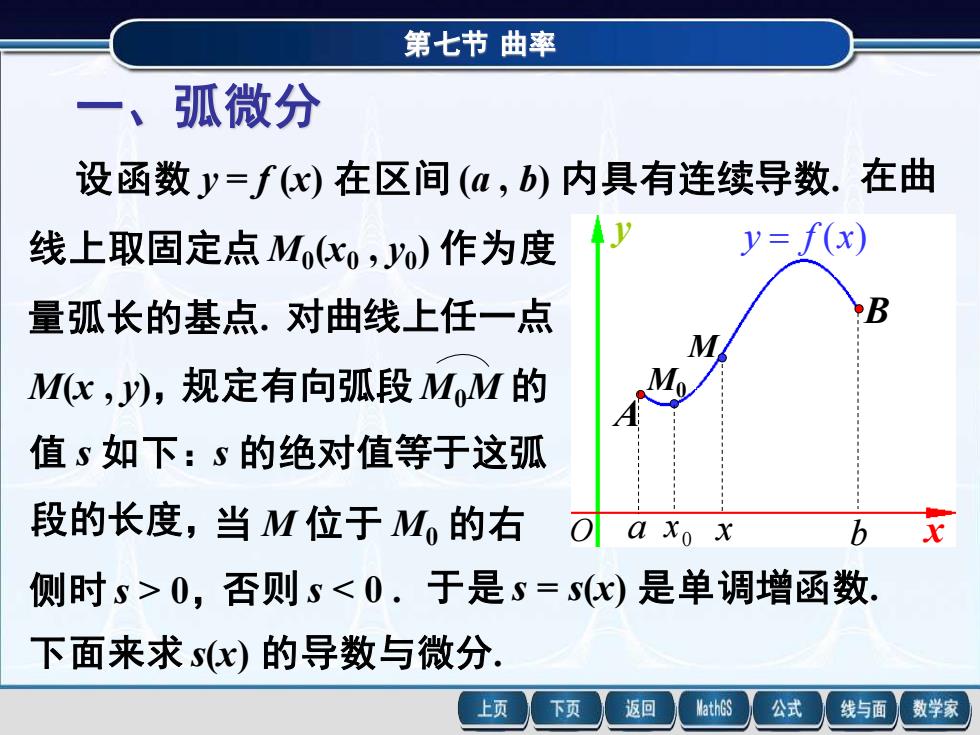
第七节曲率 一、弧微分 设函数y=fx)在区间(，b)内具有连续导数.在曲 线上取固定点Mox,yo)作为度 y=(x) 量弧长的基点.对曲线上任一点 M Mc,y),规定有向弧段MoM的 值s如下：s的绝对值等于这弧 段的长度，当M位于Mo的右 a xo x b 侧时s>0,否则s<0.于是s=sx)是单调增函数 下面来求sx)的导数与微分. 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 曲率 x y A B a b y = f (x) O 一、弧微分 设函数 y = f (x) 在区间 (a , b) 内具有连续导数. 在曲 线上取固定点 M0 (x0 , y0 ) 作为度 量弧长的基点. 对曲线上任一点 M(x , y)，规定有向弧段 M0M 的 值 s 如下：s 的绝对值等于这弧 段的长度，当 M 位于 M0 的右 侧时 s > 0，否则 s < 0 . 于是 s = s(x) 是单调增函数. M0 M 0 x x 下面来求 s(x) 的导数与微分

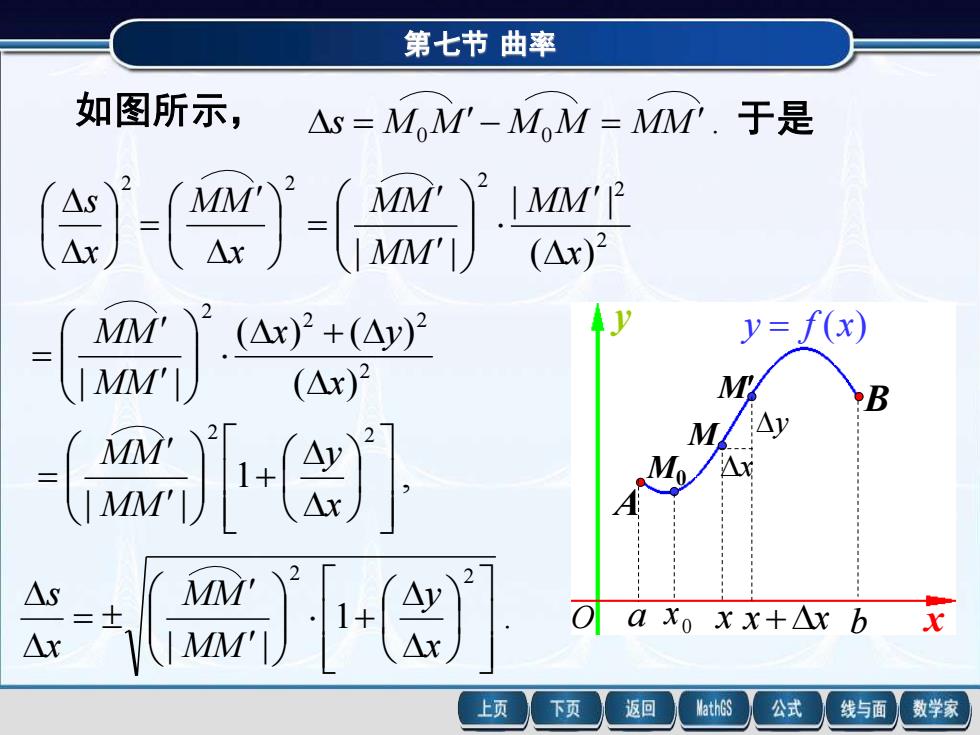
第七节曲率 如图所示， △s=MM'-MM=MM.于是 (△x)2 MM (△x)2+(△y)2 y=f(x) |MM'] (△x)2 M B M a xo xx+△xb 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 曲率 x y A B M0 M M 0 a x x x+x b y = f (x) x y O 如图所示， s = M0 M− M0 M = MM  . 于是 2         x s 2         = x MM 2 2 2 ( ) | | | | x MM MM MM              = 2 2 2 2 ( ) ( ) ( ) | | x x y MM MM   +             = 1 , | | 2 2                 +           = x y MM MM 1 . | | 2 2                  +           =    x y MM MM x s

第七节曲率 △S MM' △x MM'] △x MM' lim y 0IMM 小，im =y, y=f(x) ds M =±V1+y2 M △y dx Mo 因为S=sx)是单调增函数， 所以-V+y2, ds 于是有 dx a xo xx+△xb ds =1+ydx 弧微分 上页 下页 返回 MathGS 公式 线与面 数学家

第七节 曲率 1, | | | | lim 0 =    → MM MM x  , lim 0 y x y x =     → 1 . | | 2 2                  +           =    x y MM MM x s 1 . d d 2 y x s  =  +  因为 s = s(x) 是单调增函数， 所以 1 , d d 2 y x s = +  于是有 d 1 d . 2 s = + y  x 弧微分 x y A B M0 M M 0 a x x x+x b y = f (x) x y O

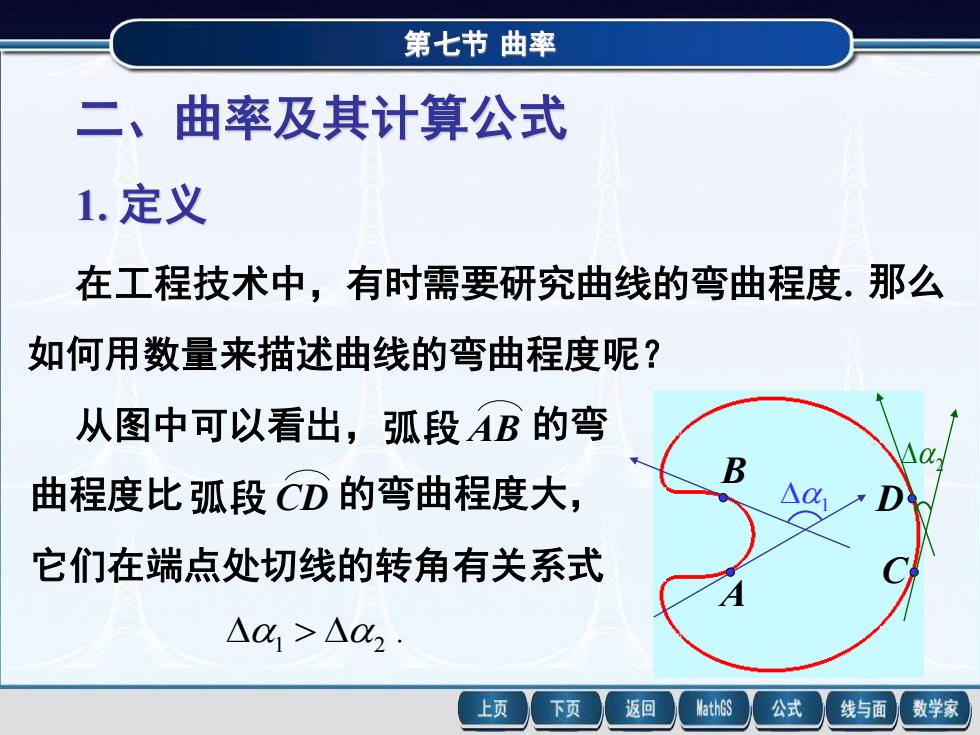
第七节曲率 二、曲率及其计算公式 1.定义 在工程技术中，有时需要研究曲线的弯曲程度.那么 如何用数量来描述曲线的弯曲程度呢？ 从图中可以看出，弧段AB的弯 曲程度比弧段CD的弯曲程度大， 它们在端点处切线的转角有关系式 △01>△C2 上页 下页 返回ath6s 公式 线与面八数学家

第七节 曲率 二、曲率及其计算公式 1. 定义 在工程技术中，有时需要研究曲线的弯曲程度. 那么 如何用数量来描述曲线的弯曲程度呢？ 1 2 A B C D 从图中可以看出，弧段 AB 的弯 曲程度比弧段 CD 的弯曲程度大， 它们在端点处切线的转角有关系式 . 1  2