
第三章 第七节曲车(Curvature) 一、孤微分 二、曲率及其计算公式 三、曲率半径与曲率圆 四、小结与思考练习 2009年7月3日星期五 1 目录 上页 下 、返回
2009年7月3日星期五 1 目录 上页 下页 返回 第七节 曲 率 第三章 二、曲率及其计算公式 (Curvature) 四、小结与思考练习 三、曲率半径与曲率圆 一、弧微分

一、孤微分Element of Length or Differential of Arc 设函数y=f(x)在区间 (a,b)内具有连续的导数, 在曲线y=f(x)上取固定点 M A(x,y)作为度量孤长的基点 对曲线上任一点M(x,y),规定: (1)依x增大的方向作为曲线的正向. (2)M=5,当有句孤段1的方向与曲线的正向 一致时s>0,相反时s<0: 显然,s=s(x)是是x的单调增加函数 2009年7月3日星期五 2 目录 上页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 一、弧微分( Element of Length or Differential of Arc ) A 0 x M x x y o 设函数 y fx = ( ) 在区间 (,) a b 内具有连续的导数, 在曲线 y f = ( ) x 上 取固定 点 0 0 A(, ) x y 作为度量弧长的基点 对曲线上任一点 M (, ) x y ,规定: (1)依 x 增大的方向作为曲线的正向. (2) q AM s = ,当有向弧段 q AM 的方向与曲线的正向 一致时 s >0,相反时s <0. 显然, s = s x( )是是 x 的单调增加函数.
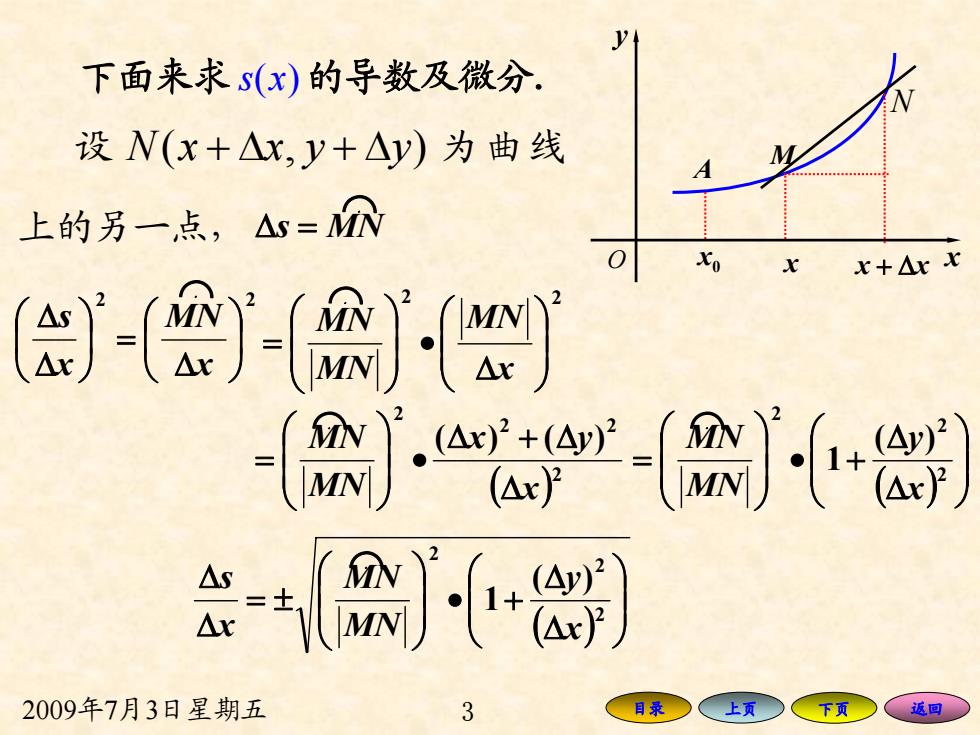
下面来求s(x)的导数及微分. 设N(x+△x,y+△y)为曲线 上的另一点,△= x+△x (-(】 -等+ 如-中】 2009年7月3日星期五 3 目录 上页 返回
2009年7月3日星期五 3 目录 上页 下页 返回 下面来求 s( ) x 的导数及微分. 设 Nx xy y (, ) +Δ +Δ 为曲线 上的另一点, A 0 x M x x y O N + Δxx Δ = MNs j 2 2 ⎟⎠⎞ ⎜⎝⎛ Δ ⎟ = ⎠⎞ ⎜⎝⎛ ΔΔ x MN xs j 2 2 ⎟⎟⎠⎞ ⎜⎜⎝⎛ Δ • ⎟⎟⎠⎞ ⎜⎜⎝⎛ = x MN MN MNj ( )2 2 2 2 )()( x yx MN MN Δ Δ+Δ • ⎟⎟⎠⎞ ⎜⎜⎝⎛ = j ( ) ⎟⎟⎠⎞ ⎜⎜⎝⎛ ΔΔ +• ⎟⎟⎠⎞ ⎜⎜⎝⎛ = 22 2 )( 1 xy MN MN j ( ) ⎟⎟⎠⎞ ⎜⎜⎝⎛ ΔΔ +• ⎟⎟⎠⎞ ⎜⎜⎝⎛ ±= ΔΔ 22 2 )( 1 xy MN MN xs j
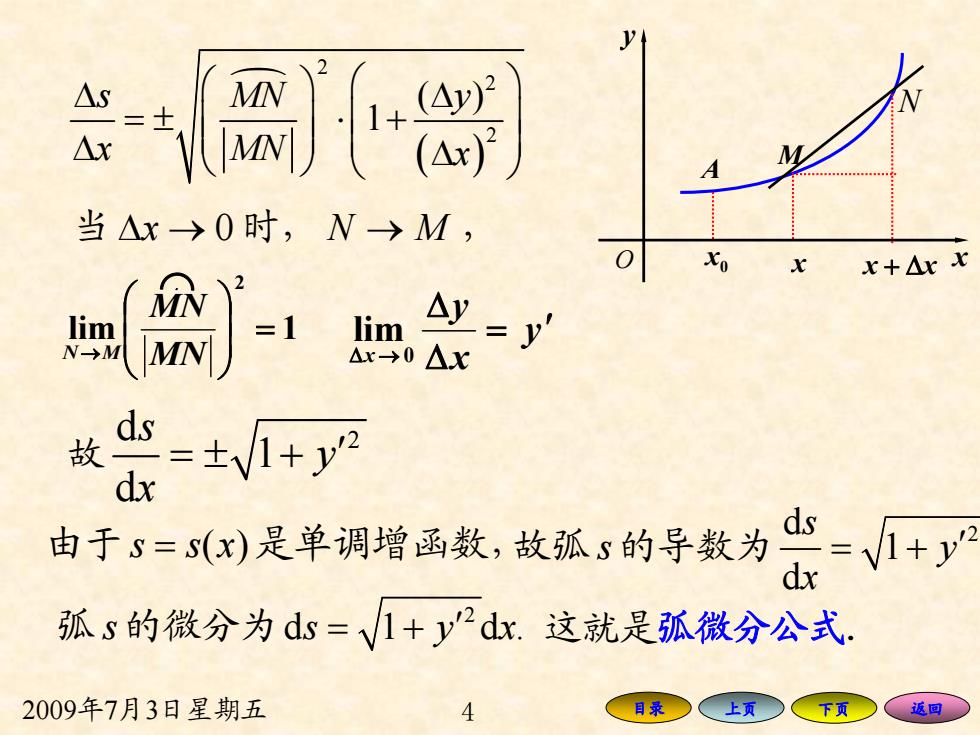
当△x→0时,N→M, x+△xx N lim Ay=y' Ax→0△X 故s=±+y dx 由于s=()是单调增函数,故孤的导数为 =1+y x 孤s的微分为ds=V1+ydx.这就是弧微分公式 2009年7月3日星期五 4 目录 上页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 q ( ) 2 2 2 ( ) 1 s MN y x MN x Δ Δ ⎛ ⎞ ⎛ ⎞ =± ⋅ + ⎜ ⎟ ⎜ ⎟ Δ ⎜ ⎟ ⎝ ⎠ ⎜ ⎟ Δ ⎝ ⎠ A 0 x M x x y O N + Δxx 当 Δx → 0 时, N M → , lim 1 2 = ⎟⎟⎠⎞ ⎜⎜⎝⎛ → MN MN MN j y xy x = ′ ΔΔ →Δ 0 lim 故 d 2 1 d s y x =± + ′ 由于 s = s x( )是单调增函数,故弧 s 的导数为 d 2 1 ds y x = + ′ 弧 s 的微分为 2 d 1 d. s y = + ′ x 这就是弧微分公式.

二、曲率及其计算公式(Curvature and Formula) 1曲率的定义 -描述曲线局部性质(弯曲程度)的量。 Aa. △S M M 1)孤段弯曲程度越大转角越大, 2)转角相同孤段越短弯曲程度越大。 2009年7月3日星期五 5 目录 上页 返回
2009年7月3日星期五 5 目录 上页 下页 返回 二、曲率及其计算公式 (Curvature and Formula) -描述曲线局部性质(弯曲程度)的量。 M1 M3 )Δα2 M2 ΔS2 ΔS1 M M′ ΔS1 ΔS2 N N′ )Δα 1)弧段弯曲程度越大转角越大, αΔ 1 ) 2)转角相同弧段越短弯曲程度越大。 1 曲率的定义