
2.4函数的微分及其应用 2.4.1微分及其几何意义 2.4.2微分的基本公式与运算法则 2.4.3一阶微分形式不变性 2.4.4微分在近似计算中的应用
2.4 函数的微分及其应用 2.4.1 微分及其几何意义 2.4.2 微分的基本公式与运算法则 2.4.3 一阶微分形式不变性 2.4.4 微分在近似计算中的应用
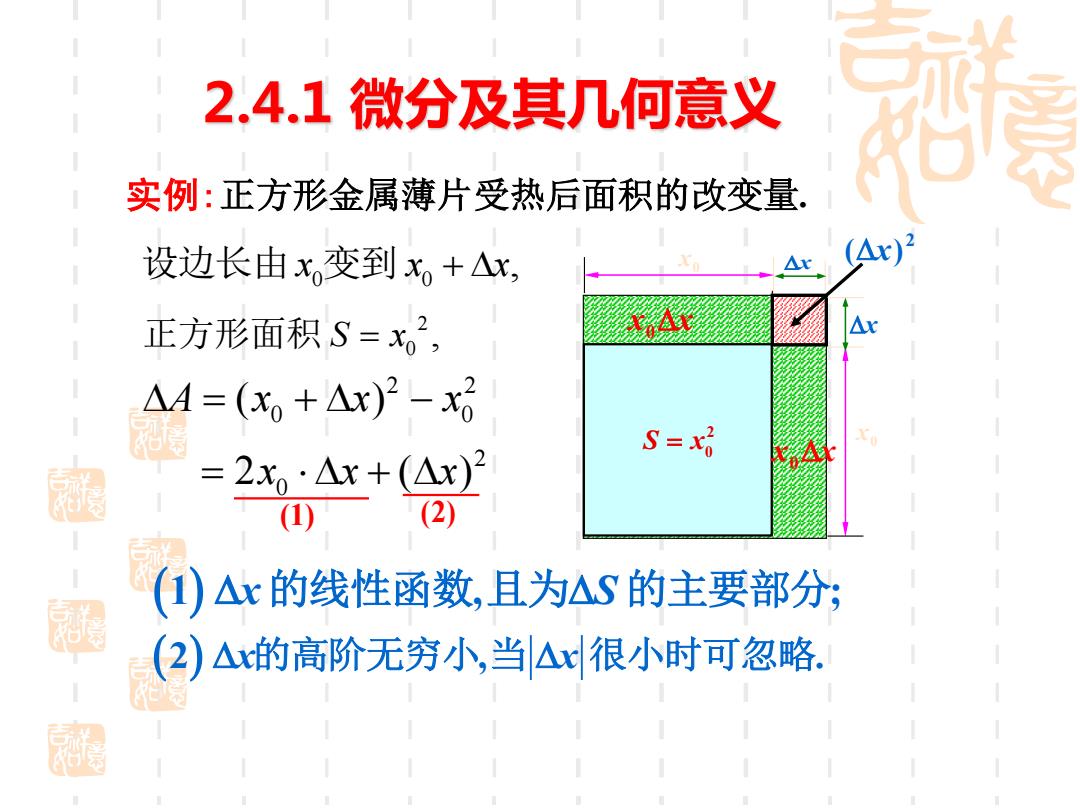
2.4.1微分及其几何意义 实例:正方形金属薄片受热后面积的改变量 设边长由x,变到x。+△x (△x)2 正方形面积S=x,2, A △A=(x,+△x)2-x S=哈 =2x·△x+(△x) e Ak (1) (2) ()△x的线性函数,且为△S的主要部分; (2)△x的高阶无穷小,当△x很小时可忽略
实例:正方形金属薄片受热后面积的改变量. 2 S x = 0 0 x 0 x 0 0 设边长由x x x 变到 + , 2 0 正方形面积 S x = , 2 2 0 0 = + − A x x x ( ) 2 0 = + 2 ( ) x x x (1) (2) (1 , ; ) x S 的线性函数 且为 的主要部分 (2 , . ) x x 的高阶无穷小 当 很小时可忽略 x x 2 (x) x x 0 x x 0 2.4.1 微分及其几何意义

再如,设函数y=x3在点x处的改变量 为△时,求函数的改变量△y. △y=(x+△x)3-x =3x·△x+3x·(△x)2+(△x) (1) (2) (1)△x的线性函数,且为△S的主要部分; (2)当△x很小时,是△x的高阶无穷小o(△x), 涵 既容易计算 ∴△y≈3x·△x. 又是较好的 近似值 问题:这个线性函数(改变量的主要部分)是否所有函 数的改变量都有?它是什么?如何求?
再如, , . 0 3 x y y x x = 为 时 求函数的改变量 设函数 在点 处的改变量 3 0 3 0 y = (x + x) − x 3 3 ( ) ( ) . 2 3 0 2 = x0 x + x x + x (1) (2) 3 . 2 0 y x x (2) , ( ), 当 x x o x 很小时 是 的高阶无穷小 问题:这个线性函数(改变量的主要部分)是否所有函 数的改变量都有?它是什么?如何求? (1 , ; ) x S 的线性函数 且为 的主要部分 既容易计算 又是较好的 近似值

1.微分定义 定义2-6设函数y=f(x)在某区间内有定义 x,及x。+△x在这区间内,如果 Ay=f(x+△x)-f(x)=A·△x+o(△x) 成立(其中A是与△x无关的常数),则称函数 =f()在点x,可微,并且称A△为函数 Iy=f(x)在点x,相应于自变量增量△x的微分 记作d或df(x方即妙 =A△x. 微分dy叫做函数增量△y的线性主部.(微分的实质)
定义2-6 0 0 0 0 0 0 0 0 0 ( ) , , ( ) ( ) ( ) ( ), ( ) , ( ) , ( ), . x x x x y f x x x x y f x x f x A x o x A x y f x A x y f x x x dy df x dy A x x = = = + = + − = + = = = 设函数 在某区间内有定义 及 在这区间内 如果 成立 其中 是与 无关的常数 则称函数 并且称 为函数 在点 相应于自变量增 在点 可微 量 的微分 记作 或 即 微分dy叫做函数增量y的线性主部. (微分的实质) 1. 微分定义

△y=f(x,+△x)-f(x)=A·△x+o(A),yx==A△x 由定义2-6知: (y是自变量的改变量卧x的线性函数 (2)△y-y=o(△x)是比△x高阶无穷小; (3)当A≠0时,与△y是等价无穷小 .y=1+ (△x) →1( △x→0) y A·△x (4)A是与△x无关的常数但与f(x)和x,有关 湖 (⑤)当△x很小时,△y≈(线性主部, 腿
由定义2-6知: (1) dy是自变量的改变量x的线性函数; (2) y − dy = o(x)是比x高阶无穷小; (3)当A 0时,dy与y是等价无穷小; dy y A x o x = + ( ) 1 → → 1 ( 0). x (4) , ( ) ; A是与x无关的常数 但与f x 和x0有关 (5)当x很小时,y dy (线性主部). 0 0 = + − = + y f x x f x A x o x ( ) ( ) ( ), 0 . x x dy A x = =