
1.3函数的连续性 1.3.1连续性的概念 1.3.2函数的间断点 1.3.3连续函数的运算与初等函 涵 数的连续性 1.3.4闭区间上连续函数的性质
1.3.1 连续性的概念 1.3.3 连续函数的运算与初等函 数的连续性 1.3 函数的连续性 1.3.2 函数的间断点 1.3.4 闭区间上连续函数的性质
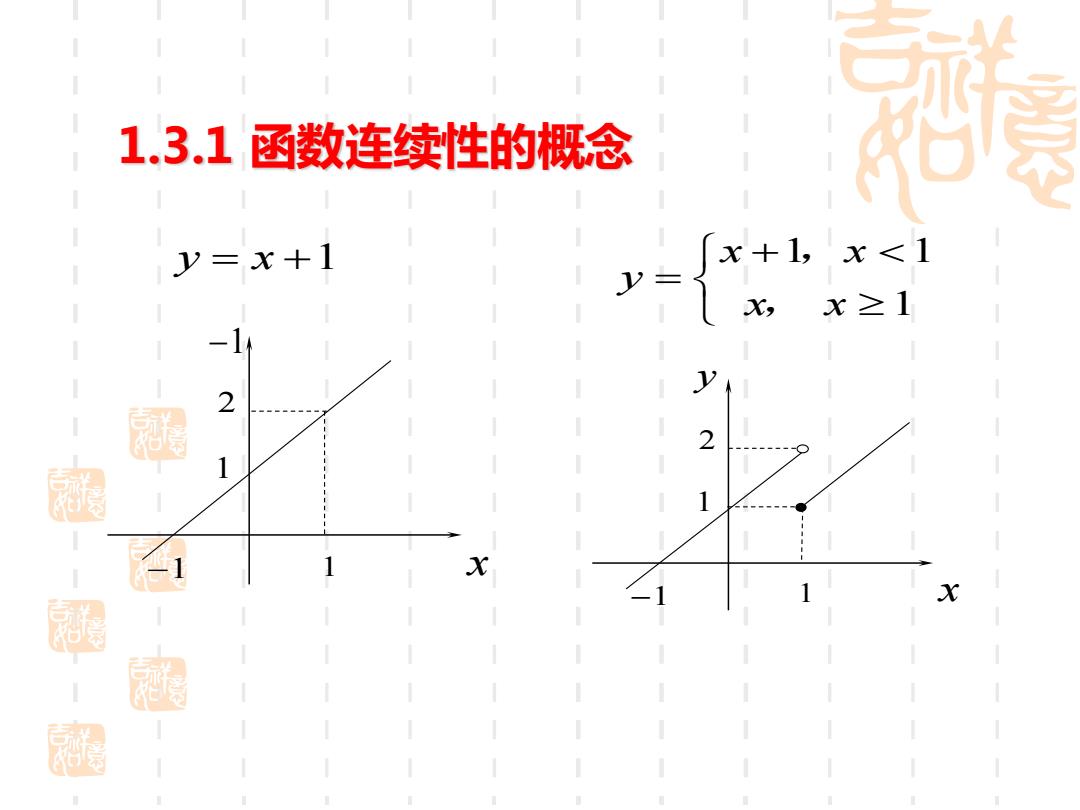
1.3.1函数连续性的概念 y=x+1 x+1,x<1 x,x≥1 -1 2 X 酸
−1 1 x 1 2 −1 y x = +1 1 1 1 x x y x x + = , , y 1 x 1 2 −1 1.3.1 函数连续性的概念

1.3.1函数连续性的概念 1.变量的增量 研究函数y=x2,当x从初值1增加到 终值1.1,函数值y从1增加到1.21,我们把1.1 -1=0.1称为自变量的增量,把1.21-1= 0.21称为函数y的增量
1. 变量的增量 研究函数 y=x 2,当x从初值1增加到 终值1.1,函数值 y从1增加到1.21,我们把1.1 -1=0.1称为自变量的增量,把1.21-1= 0.21称为函数 y 的增量。 1.3.1 函数连续性的概念

1.变量的增量 般地,常用o表示自变量的初值,用 △x表示自变量的增量,则自变量的终值可 表示为x+△x,相应地 用△y表示函数值的增量 y=f(x) 则 y 湖 △y=fx+△x)-fx0) △x 0 xo+△xX
x0 x0 + x 一般地, 常用x0 表示自变量的初值,用 △x表示自变量的增量,则自变量的终值可 表示为x0+△x,相应地 用△y表示函数值的增量, △y=f( x0+△x)-f(x0 ) 则 x y 0 y = f (x) x y 1. 变量的增量

2.函数连续性的定义 定义1-10设函数y=f(x)在x的某一邻域内有定 义,如果当自变量在点x,处的增量△x→0时 有 lin Ay=limf(+x)-f()=0 A→0 则称y=f(x)在点x处连续,称x为连续点 函数在x处连续的意义是指:当自变量在x处的增量 △x为无穷小量时,函数的增量△y也为无穷小量。 【这一定义说明了连续的本质:当自变量变化很微小 时,函数值相应变化也很微小
0 0 0 0 0 0 0 0 ( ) 0 lim lim[ ( ) ( )] 0 ( ) x x y f x x x x y f x x f x y f x x x → → = → = + − = = 设函数 在 的某一邻域内有定 义,如果当自变量在点 处的增量 时, 有 则称 在点 处连续,称 为连续点。 函数在x0处连续的意义是指:当自变量在x0处的增量 △x为无穷小量时,函数的增量△y也为无穷小量。 这一定义说明了连续的本质:当自变量变化很微小 时,函数值相应变化也很微小. 2. 函数连续性的定义 定义1-10