
第4章多元函数微积分学 4.1空间解析几何简介 4.2多元函数的概念 4.3二元函数的极限与连续 4.4偏导数与全微分 涵 4.5二元复合函数和隐函数的微分法 4.6二元函数的极值 4.7二重积分
第4章 多元函数微积分学 4.1 空间解析几何简介 4.2 多元函数的概念 4.3 二元函数的极限与连续 4.4 偏导数与全微分 4.5 二元复合函数和隐函数的微分法 4.6 二元函数的极值 4.7 二重积分

4.1空间解析几何简介 4.1.1空间直角坐标系的建立 4.1.2 空间两点间的距离 涵 4.1.3常见的空间曲面
4.1 空间解析几何简介 4.1.1 空间直角坐标系的建立 4.1.2 空间两点间的距离 4.1.3 常见的空间曲面
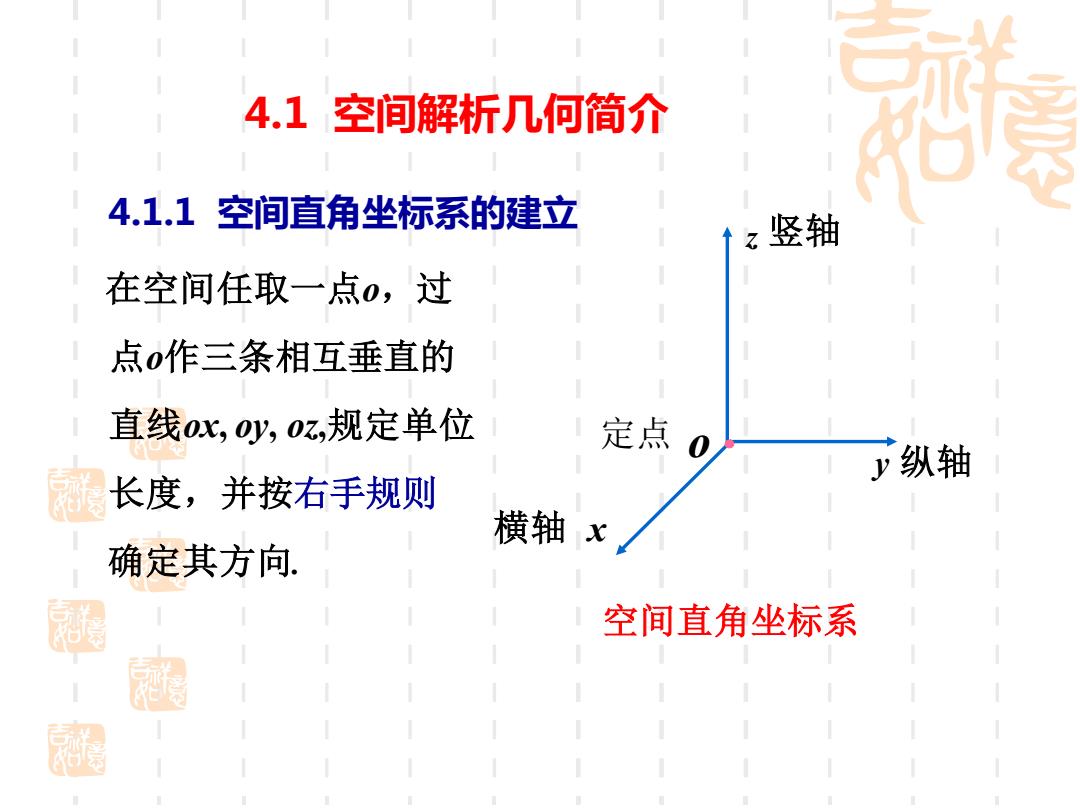
4.1空间解析几何简介 4.1.1空间直角坐标系的建立 z竖轴 在空间任取一点0,过 点o作三条相互垂直的 直线0K,0y,0z,规定单位 定点 0 y纵轴 长度,并按右手规则 横轴x 确定其方向 空间直角坐标系
4.1.1 空间直角坐标系的建立 横轴 x y 纵轴 z 竖轴 定点 o • 空间直角坐标系 在空间任取一点o,过 点o作三条相互垂直的 直线ox, oy, oz,规定单位 长度,并按右手规则 4.1 空间解析几何简介 确定其方向
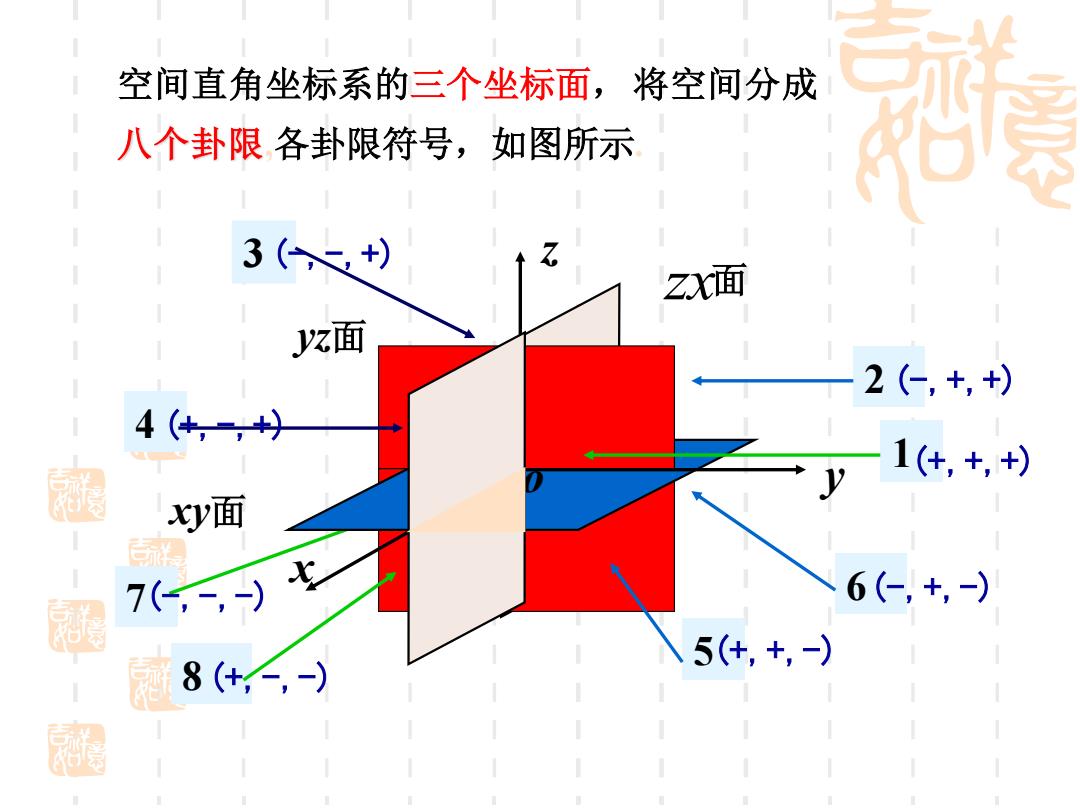
空间直角坐标系的三个坐标面,将空间分成 八个卦限各卦限符号,如图所示 3(+) Zx面 z面 2(-,+,+) 4(4,,+ 1(+,+,+) y面 7,,-) 6(-,+,-) 5(+,+,-) 8(+2,-)
7(-,-,-) xy面 yz面 空间直角坐标系的三个坐标面,将空间分成 zx 面 x o y z 2 (-,+,+) 3 (-,-,+) 5(+,+,-) 6(-,+,-) 8(+,-,-) 1(+,+,+) 4 (+,-,+) 八个卦限,各卦限符号,如图所示
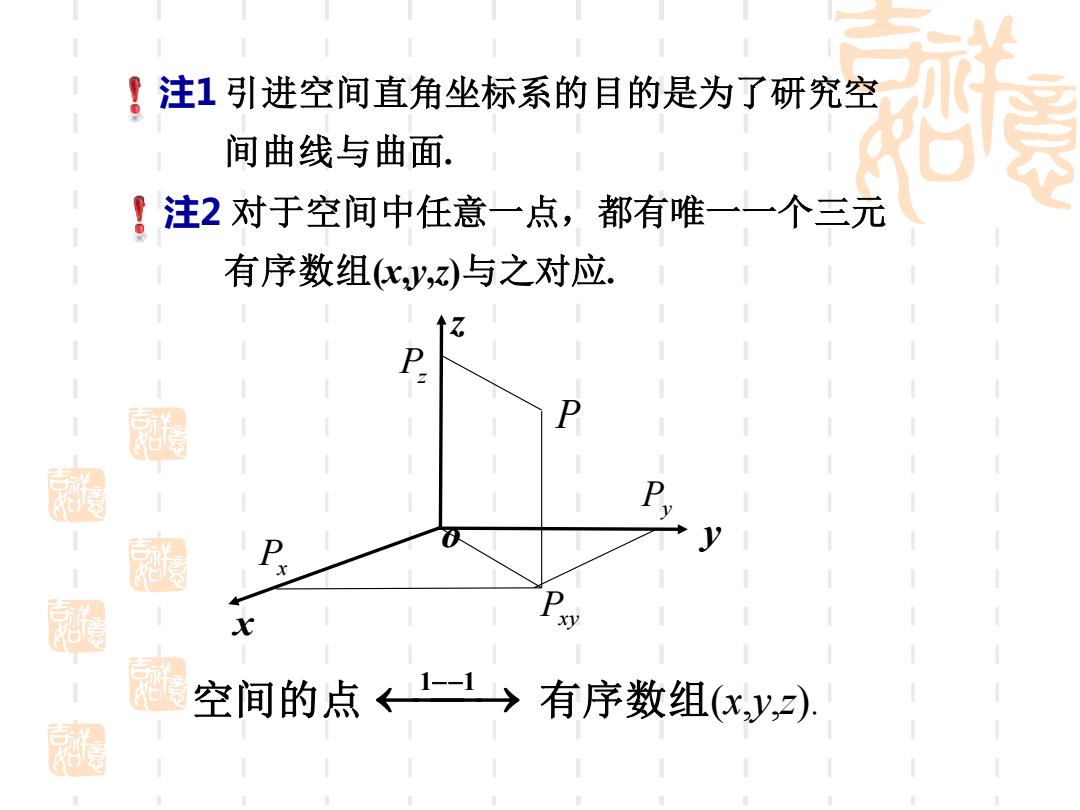
·注1引进空间直角坐标系的目的是为了研究空 间曲线与曲面 注2对于空间中任意一点,都有唯一一个三元 有序数组化y,z)与之对应. D 涵 极食 空间的点←一1→有序数组(x,y,)
注1 引进空间直角坐标系的目的是为了研究空 注2 对于空间中任意一点,都有唯一一个三元 x o y z P P xy P x P y P z 空间的点 ⎯→ 有序数组(x,y,z). 1−−1 间曲线与曲面. 有序数组(x,y,z)与之对应