
对生标的曲面积分△S在xOy面上的投影(△S)xy,实际上就是AS在xOy面上的投影区域的面积附以一定的正负号。类似地,可定义△S在vOz面及zOx面的投影:(△S) yz, (AS)z→α,β恰好等于△S与坐标面yOz、zOx的二面角
类似地,可定义 S 在yOz面及zOx面的投影: ( ) , S yz , ( ) , S 在xOy面上的投影 S xy S 在xOy面上的投影区域的面积附以一定的 实际上就是 正负号. S zx ( ) 恰好等于S与坐标面yOz、zOx 的二面角. 对坐标的曲面积分
对生标的曲面积分概念的引入二、实例流向曲面一侧的流量(1)流速场为常向量,有向平面区域A.求单位时间流过A的流体的质量Φ(假定密度为1)(斜柱体体积)流量@= A||cos V= Ai.n0nn为平面A的单位法向量
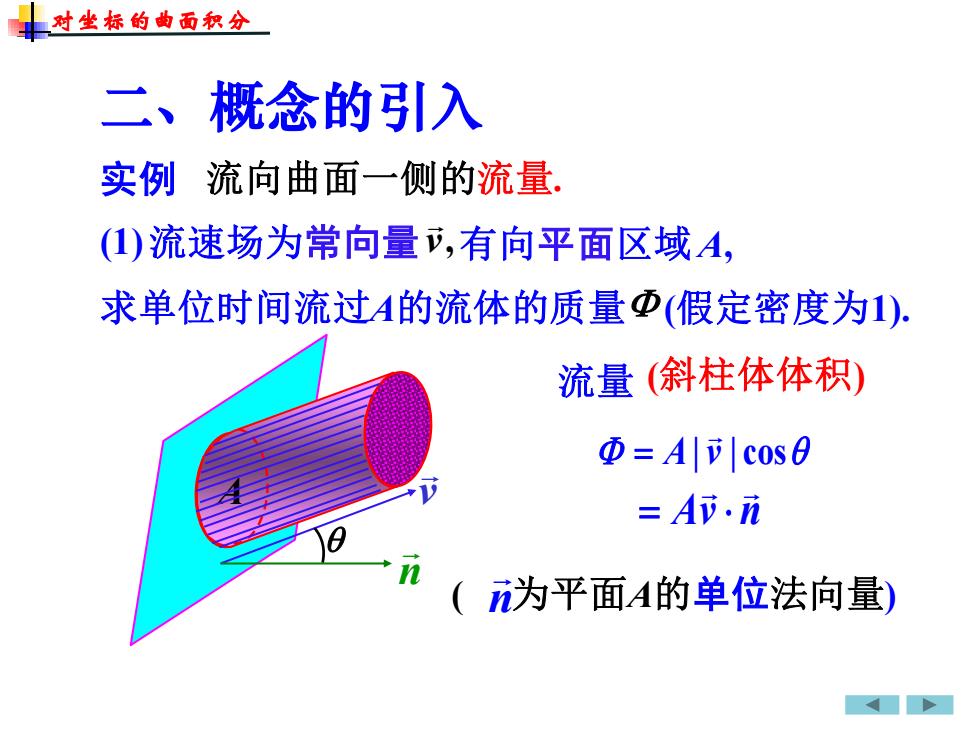
流向曲面一侧的流量. v A| v | cos = 流量 实例 ( n 为平面A的单位法向量) (斜柱体体积) Av n = (1)流速场为常向量 v, 有向平面区域 A, 求单位时间流过A的流体的质量 (假定密度为1). 对坐标的曲面积分 二、概念的引入 A n

对尘标的曲面积分当不是常量,向曲面(2)设稳定流动的假定密度为1)不可压缩流体的速度场由流体的密度与速度z)k均不随时间而变化i(x, y,z) = P(x, y,z)给出,Z是速度场中的一片有向曲面,函数P(x, y,z), Q(x, y,z), R(x, y,z)都在上连续,求在单位时间内流向指定侧的流体的质量Φ
(2) 设稳定流动的不可压缩流体 v x y z P x y z i Q x y z j R x y z k ( , , ) = ( , , ) + ( , , ) + ( , , ) 给出, 函数 P(x, y,z), Q(x, y,z), R(x, y,z) 都在上连续, 流体的密度与速度 均不随时间而变化 (假定密度为1) 的速度场由 v 当 不是常量, 有向 曲面 求在单位 时间内流向 指定侧的 流体的质量 . 是速度场中的一片有向曲面, 对坐标的曲面积分
对尘标的曲面积分分割把曲面汾成n小块AS(△S,同时也代表第小块曲面的面积,在△S,上任取一点TV(Si,Ni,S,),nAS(5,,ni,S)福则该点流速为,,冈法向量为n.., = v(Si,Ni,S)= P(5,ni,S)i +Q(5i,n,S)j+ R(5,n,S)k
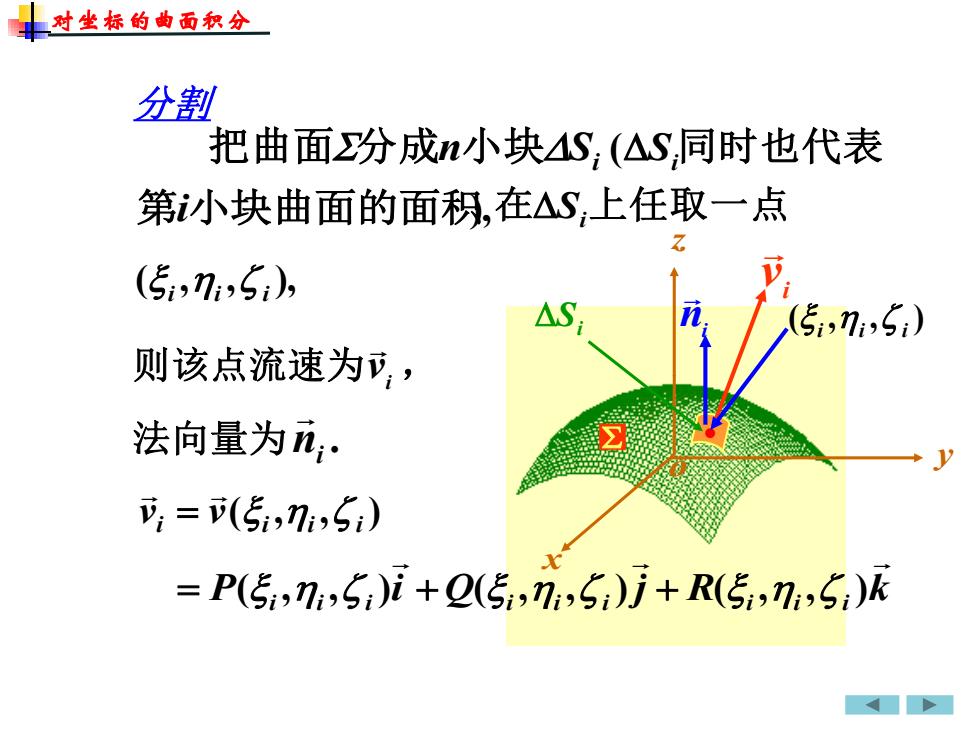
x y z o Si i v ni 分割 则该点流速为 vi , 法向量为 . ni • ( , , ) i i i 把曲面分成n小块Si (Si 同时也代表 第i小块曲面的面积),在Si 上任取一点 ( , , ), i i i ( , , ) i i i i v v = P i i i i Q i i i j R i i i k = ( , , ) + ( , , ) + ( , , ) 对坐标的曲面积分

对尘标的曲面积分常向量.有向平面@=Alilcose= Av·n该点处曲面的单位法向量n, = cosα,i + cos β,j+ cos,k取近似通过入S,流向指定侧的流量的近似值为AΦ, ~v, Icos(v,n,)AS, = v, n,As高底(i = 1,2, .", n)求和通过Z流向指定侧的流量@~Ev.n,ASi=1
常向量,有向平面 i 求和 = n i i ni Si v 1 取近似 该点处曲面Σ的单位法向量 通过Si流向指定侧的流量的近似值为 i ni Si = v 高 底 (i = 1,2, ,n). Si A| v | cos = Av n = 对坐标的曲面积分 通过Σ流向指定侧的流量 ni i i i j ik = cos + cos + cos | | cos( , ) i i ni v v