
曲率第七节一、弧微分曲率及其计算公式三、曲率圆与曲率半径*四、曲率中心的计算公式渐屈线与渐伸线
第七节 曲率 一、弧微分 三、曲率圆与曲率半径 二、曲率及其计算公式 *四、曲率中心的计算公式 渐屈线与渐伸线
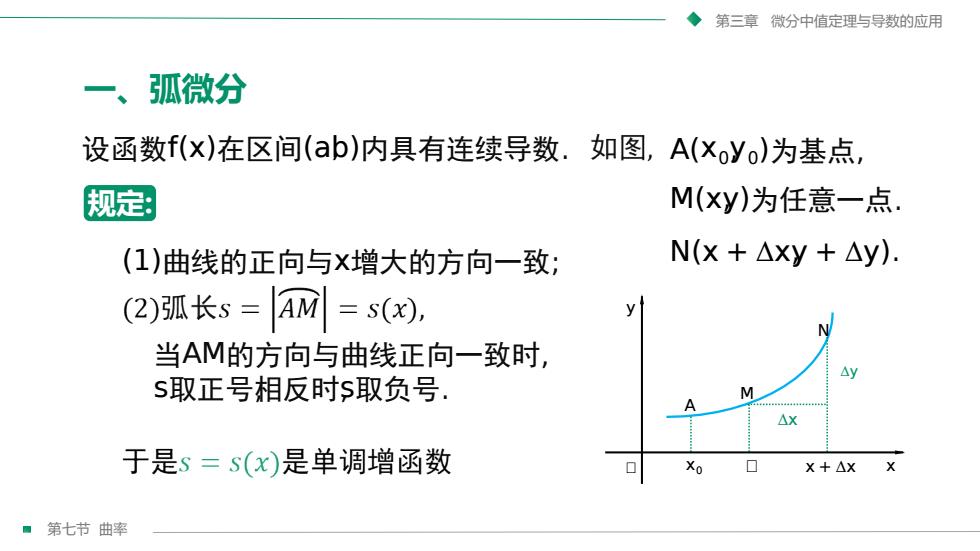
第三章微分中值定理与导数的应用一、弧微分设函数f(x)在区间(ab)内具有连续导数.如图,A(xoyo)为基点,M(xy)为任意一点,规定:N(x + △xy + y)(1)曲线的正向与x增大的方向一致;(2)弧长s =AM= s(x),y当AM的方向与曲线正向一致时Ays取正号相反时s取负号,MYAx于是s=s(x)是单调增函数口Xo0xX + △x第七节曲率
第七节 曲率 第三章 微分中值定理与导数的应用 一、弧微分 A x0 M ᵰ x + Δx x y ᵰ 规定: 设函数f(x)在区间(a,b)内具有连续导数. (1)曲线的正向与x增大的方向一致; 当AM的方向与曲线正向一致时, s取正号,相反时,s取负号. A(x0,y0)为基点, M(x,y)为任意一点. N(x + Δx,y + Δy). N Δx Δy
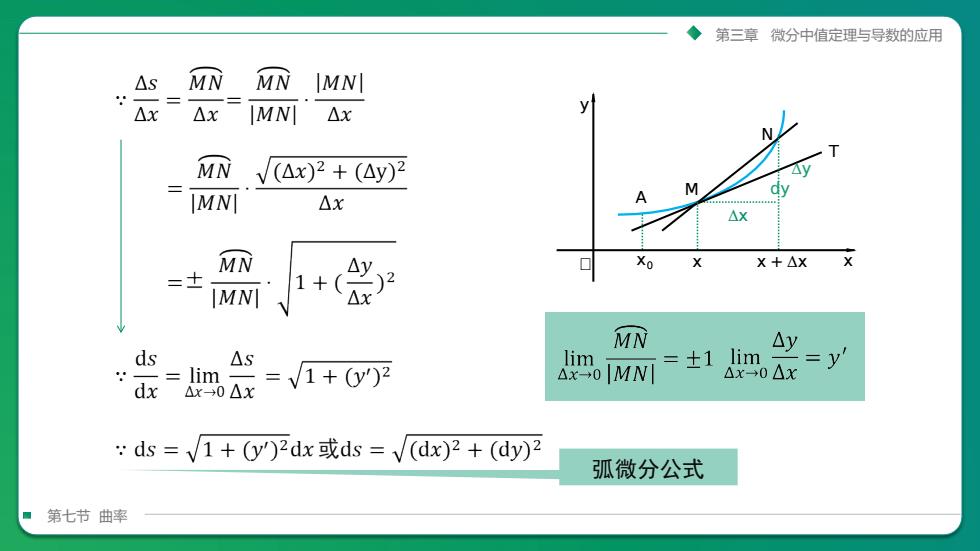
第三章微分中值定理与导数的应用MNMNAsIMN]yAx[MN]AxAxMN/(△x)? + (Ay)M1A[MN]AxAx+MNXoxX + △x口MNMNAydsAsJimlim±1AX-0MNAx-0Axlim1+(y)3dxAx-0△x:ds=/1+(y)2dx或ds=(dx)2+(dy)2弧微分公式第七节曲率
第七节 曲率 第三章 微分中值定理与导数的应用 弧微分公式 N T A x0 M x x + Δx x y ᵰ Δx Δy dy 第三章 微分中值定理与导数的应用 第七节 曲率
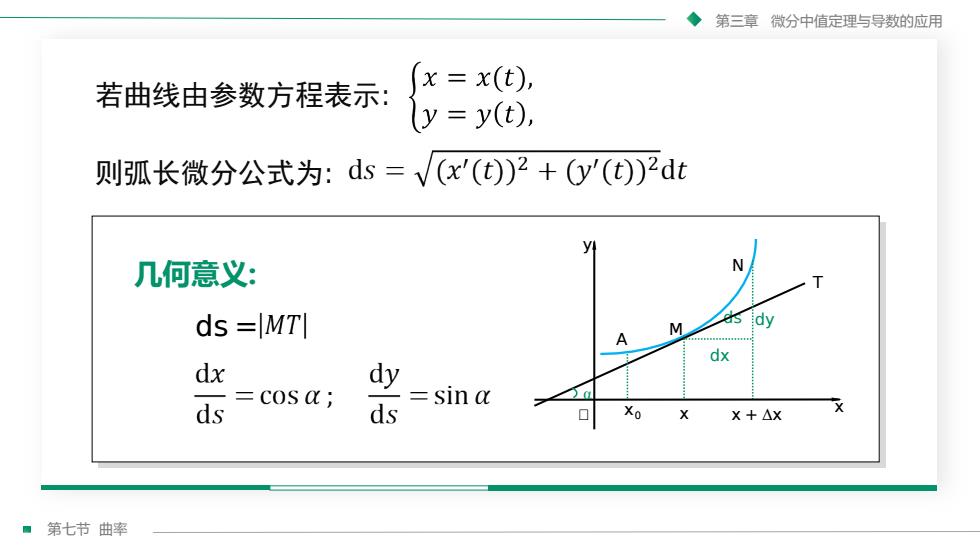
第三章微分中值定理与导数的应用(x = x(t),若曲线由参数方程表示:(y = y(t),则弧长微分公式为:ds=/(x'(t))2+(y'(t))2dtyN几何意义:idyds =|MTIMAdxdxdysina=cosα;?xdsdsXo口xX +△x第七节曲率
第七节 曲率 第三章 微分中值定理与导数的应用 则弧长微分公式为: 几何意义: 若曲线由参数方程表示: dx ds dy N T A x0 M x x + Δx x y ᵰ α ds =
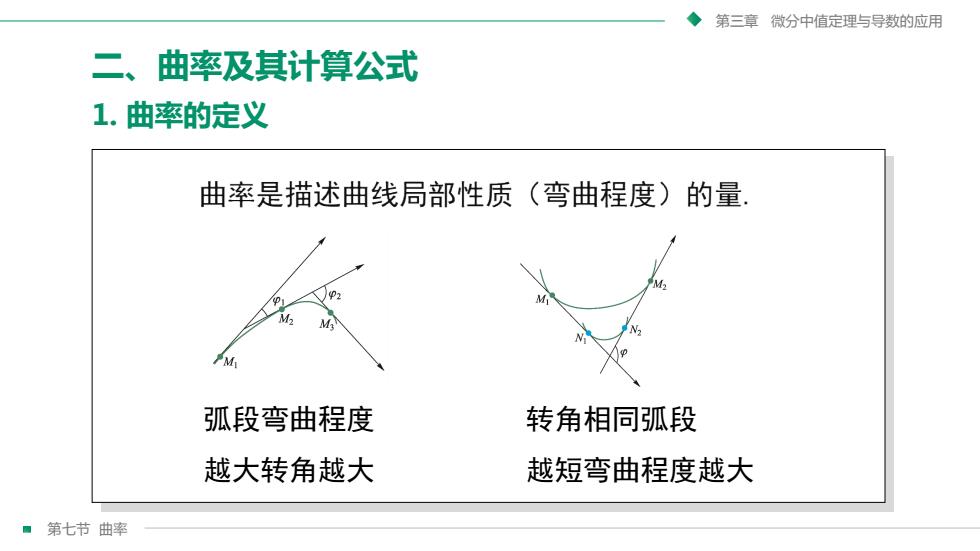
第三章微分中值定理与导数的应用曲率及其计算公式二E1.曲率的定义曲率是描述曲线局部性质(弯曲程度)的量MMM弧段弯曲程度转角相同弧段越大转角越大越短弯曲程度越大第七节曲率
第三章 微分中值定理与导数的应用 第七节 曲率 二、曲率及其计算公式 弧段弯曲程度 越大转角越大 转角相同弧段 越短弯曲程度越大 1. 曲率的定义