
d(e*) = e*dxd(a*) = a* In adx1d(ln x) = -dxdxd(log, x) =xlnax11dxdxd(arcsin x) =d(arccos x) =V1-x?V1-x?1dxdxd(arctan x)d(arccotx) =.21+x1+x2.函数和、差、积、商的微分法则du±v)=du±dyd(Cu) = Cduvdu-udyd(=) :d(uv) = vdu+ udy二
2 2 2 2 d( ) ln d d( ) d 1 1 d(log ) d d(ln ) d ln 1 1 d(arcsin ) d d(arccos ) d 1- 1- 1 1 d(arctan ) d d(arccot ) d 1 1 x x x x a a a a x e e x x x x x x a x x x x x x x x x x x x x = = = = = = − = = − + + 2. 函数和、差、积、商的微分法则 2 d( ) d d d( ) d d d d( ) d d d( ) u v u v Cu C u u v u u v uv v u u v v v = = − = + =
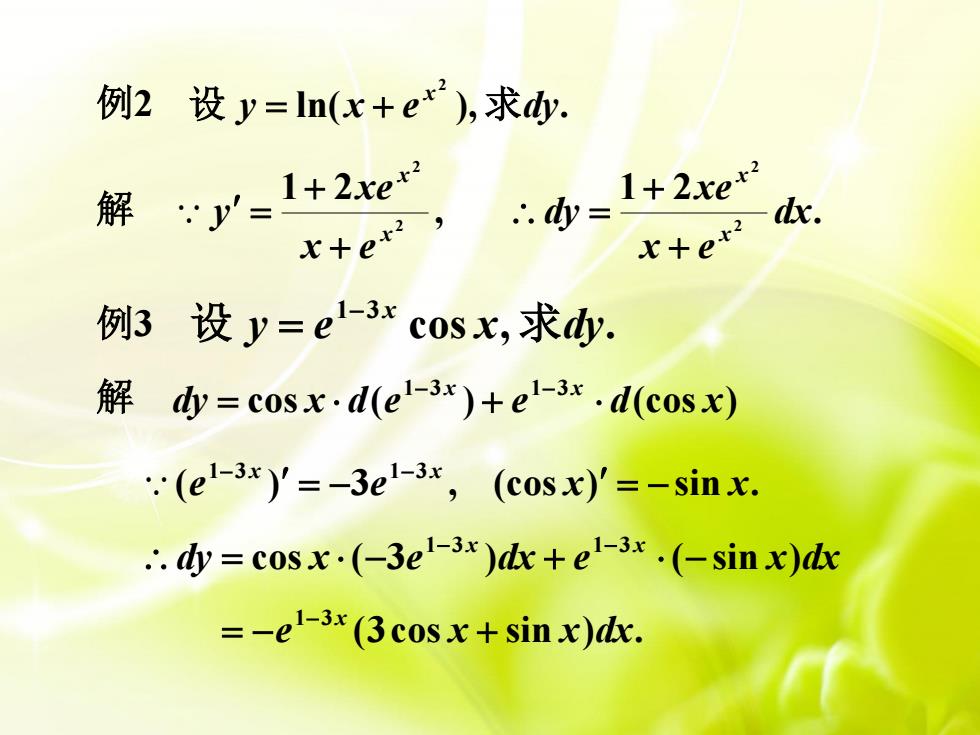
例2 设 y= In(x +e*),求dy1+2xe+1 + 2xe+?解dx... dy :..V3Petetx+ex+例3 设 y = el-3× cos x,求dy.解 dy = cosx ·d(el-3x)+el-3x .d(cosx): (el-3x)'= -3el-3x, (cosx)'= -sin x... dy = cos x ·(-3el-3*)dx + el-3x .(-sin x)dx= -el-3x (3cos x + sin x)dx
例 2 解 ln( ), . 2 y x e dy 设 = + x 求 , 1 2 2 2 x x x e xe y ++ = . 1 2 2 2 dx x e xe dy x x ++ = 例 3 解 cos , . 1 3 y e x dy 设 = − x 求 cos ( ) (cos ) 1 3 1 3 dy x d e e d x x x = + − − ( ) 3 , (cos ) sin . 1 3 1 3 e e x x x x = − = − − − dy x e dx e x dx x x cos ( 3 ) ( sin ) 1 3 1 3 = − + − − − (3cos sin ) . 1 3 e x x dx x = − + −