
2.可微的条件定理函数f(x)在点x,可微的充要条件是函数f(x)在点x,处可导,且 A= f'(x)证(1)必要性:f(x)在点x,可微o(△r)AyA-:. Ay = A . Ax + o(△xr)AxArAyo(△x)= A.则 limA+limArAr-→>0 AxAr-→0即函数f(x)在点x,可导,且A=f(x,)
0 0 0 ( ) ( ) , ( ). f x x f x x A f x = 函数 在点 可微的充要条件是函 数 在点 处可导 且 定理 证 (1) 必要性 ( ) , f x 在点x0可微 y = A x + o(x), , ( ) x o x A x y = + x o x A x y x x = + → → ( ) lim lim 0 0 则 = A. ( ) , ( ). 0 0 即函数 f x 在点 x 可导 且A = f x 2.可微的条件

(2)充分性:函数f(x)在点x可导Ay = f'(x),= f'(x0)+α,即limAr-→0 △xAr(△x → 0)从而 Ay = f'(x)·Ax+α·(Ax),: α→0= f'(x.). △x + o(△r),:函数f(x)在点x,可微,且f'(x)= A.:可导台可微A= f'(xo)函数y=f(x)在任意点x的微分,称为函数的微分,记作dy或df(x),即dy=f(x)Ax
(2) 充分性 ( ) ( ), 从而 y = f x0 x + x ( ) , = 0 + f x x y 即 ( ) , 函数f x 在点x0可导 lim ( ), 0 0 f x x y x = → → 0 (x → 0), ( ) ( ), 0 = f x x + o x ( ) , ( ) . 函数 f x 在点 x0可微 且 f x0 = A . ( ). x0 可导 可微 A = f ( ) , , ( ), ( ) . y f x x dy df x dy f x x = = 函数 在任意点 的微分 称为函数的 微分 记作 或 即

例1求函数y=x2当x=2,△x=0.02时的微分解 : dy= (x)Ax = 3xAx.= 0.24.= 3x△x.. dyx=2x=2Ax=0.02Ar=0.02通常把自变量x的增量△x称为自变量的微分记作dx,即dx =△x.dyf'(x).:. dy = f'(x)dx.dx即函数的微分dy与自变量的微分x之商等于该函数的导数.导数也叫微商
例 1 解 2, 0.02 . 求函数 y = x3 当 x x = 时的微分 dy = (x )x 3 3 . 2 = x x0.02 2 2 0.02 2 3 = = = xx xx dy x x = 0.24. , , . x x dx dx x = 通常把自变量 的增量 称为自变量的微分 记作 即 dy = f (x)dx. f (x). dx dy = . " ". 即函数的微分dy dx 与自变量的微分 之商等于 该函数的导数 导数也叫 微商
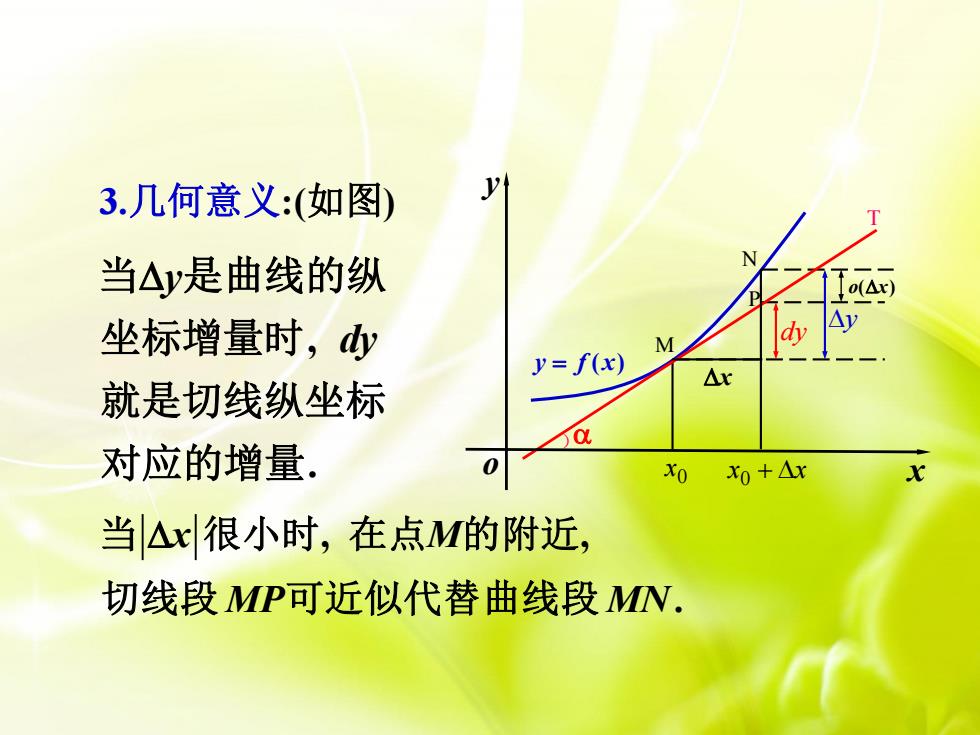
y3.几何意义:(如图)N当△y是曲线的纵To(Ar)Aydy坐标增量时,dyMy= f(x)Ar就是切线纵坐标a对应的增量0Xo+AxxXo当△x很小时,在点M的附近,切线段MP可近似代替曲线段MN
y = f (x) 0x M N T dy yo(x) ) x yo x 3.几何意义:(如图) . , 对应的增量 就是切线纵坐标 坐标增量时 当 是曲线的纵 dy y x + x 0 P , , . x M MP MN 当 很小时 在点 的附近 切线段 可近似代替曲线段

三、 微分的求法dy = f'(x)dx求法:计算函数的导数,乘以自变量的微分1.基本初等函数的微分公式d(x") = μuxu-'dxd(C) = 0d(sin x) = cos xdxd(cosx) = -sin xdxd(tan x) = sec xdxd(cot x) = -csc2 xdxd(secx) = sec x tan xdxd(cscx)=-cscxcotxdx
dy = f (x)dx 求法: 计算函数的导数, 乘以自变量的微分. 1.基本初等函数的微分公式 1 2 2 d( ) 0 d( ) d d(sin ) cos d d(cos ) sin d d(tan ) sec d d(cot ) csc d d(sec ) sec tan d d(csc ) csc cot d C x x x x x x x x x x x x x x x x x x x x x x x − = = = = − = = − = = − 三、微分的求法