
第二节定积分在几何上的应用平面图形的面积旋转体的体积三、平面曲线的孤长四、小结
第二节 定积分在几何上的应用 • 一、平面图形的面积 • 二、旋转体的体积 • 三、平面曲线的弧长 • 四、小结
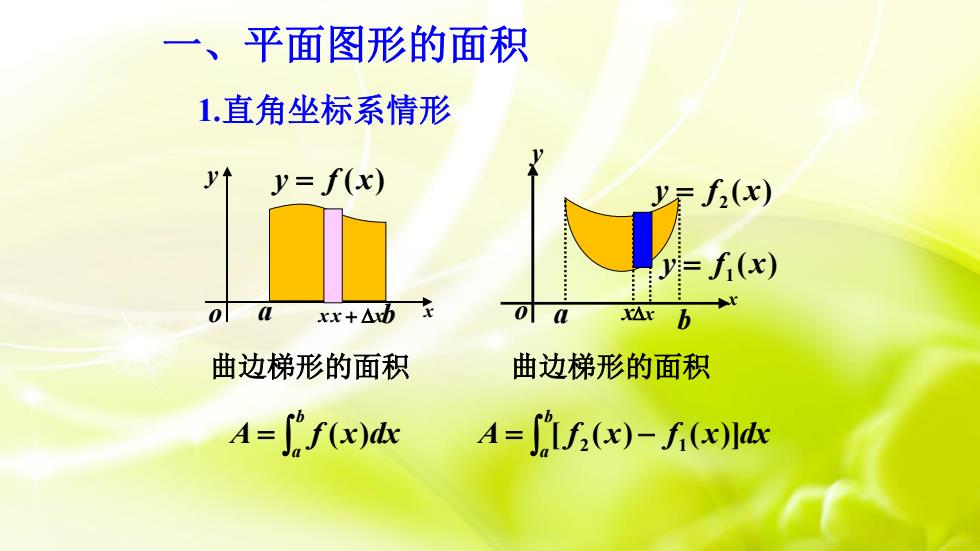
一、平面图形的面积1.直角坐标系情形yty=f(x)y=f(x)y=f.(x)X小ofoaxx+AbaxArb曲边梯形的面积曲边梯形的面积A= f'f(x)dxA= I'lf;(x)- fi(x)dx
曲边梯形的面积 = b a A f (x)dx 曲边梯形的面积 = − b a A [ f (x) f (x)]dx 2 1 x y o y = f (x) a xx + xb 1.直角坐标系情形 ( ) 1 y = f x ( ) 2 y = f x a b xx x y o 一、平面图形的面积
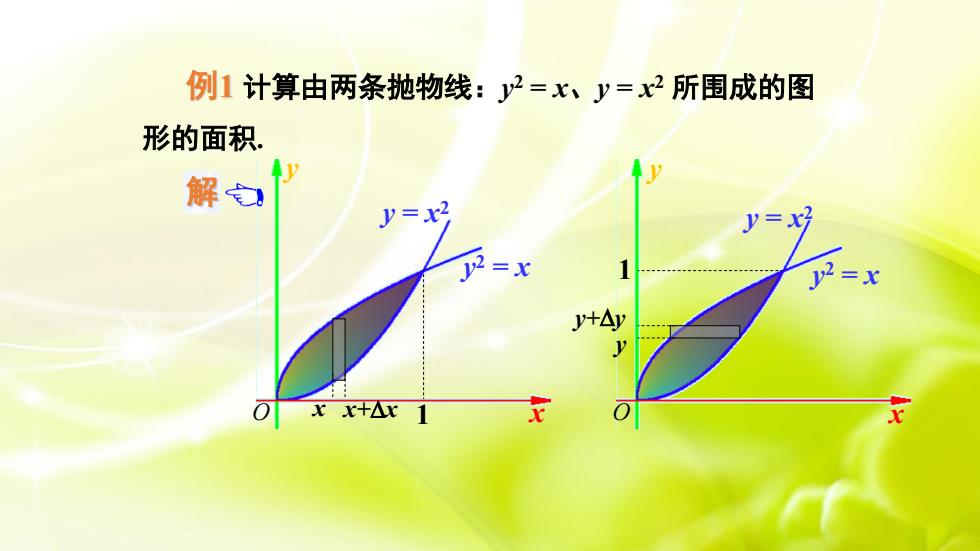
例1计算由两条抛物线:2=x、y=x2所围成的图形的面积解仓J=x2VXy2=xy2=xy+AyVOxx+ArX1+
例1 计算由两条抛物线:y 2 = x、y = x 2 所围成的图 第二节 定积分在几何上的应用 解 例1 计算由两条抛物线:y 2 = x、y = x 2 所围成的图 形的面积. 先选 x 为积分变量,其 变化范围为 [0 , 1],此时微元为 小竖条,如图所示. 面积元素为 d ( )d . 2 A = x − x x 所求面积为 = − 1 0 2 A ( x x )dx 1 0 2 3 3 3 1 3 2 = x − x . 3 1 = y 2 = x y = x 2 x y O 1 x x+x 形的面积. y 2 = x y = x 2 x y O 1 x x+x y 2 = x y = x 2 x y O 1 y y+y
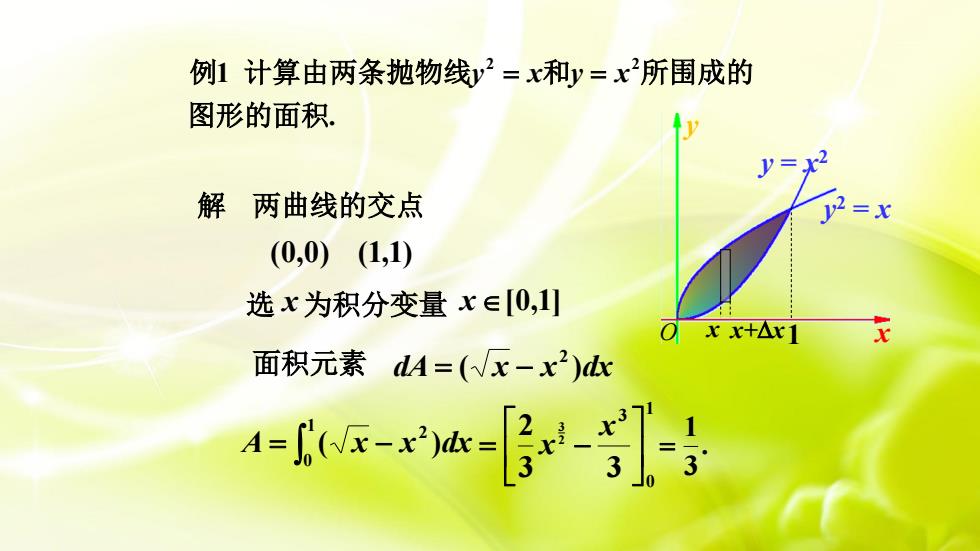
例1计算由两条抛物线2=x和y=x所围成的图形的面积y=x2解两曲线的交点y2=x(0,0)(1,1)选x为积分变量xE[0,1]xOxx+A1面积元素 dA=(Vx-x)dx[-]--A=f"(Vx-x)dx=
解 两曲线的交点 (0,0) (1,1) 面积元素 dA ( x x )dx 2 = − 选 x 为积分变量 x [0,1] A ( x x )dx 2 10 = − 10 3 3 3 2 23 = − x x . 31 = 2 2 1 . 例 计算由两条抛物线y x y x = = 和 所围成的 图形的面积 y 2 = x y = x 2 x y O 1 x x+x
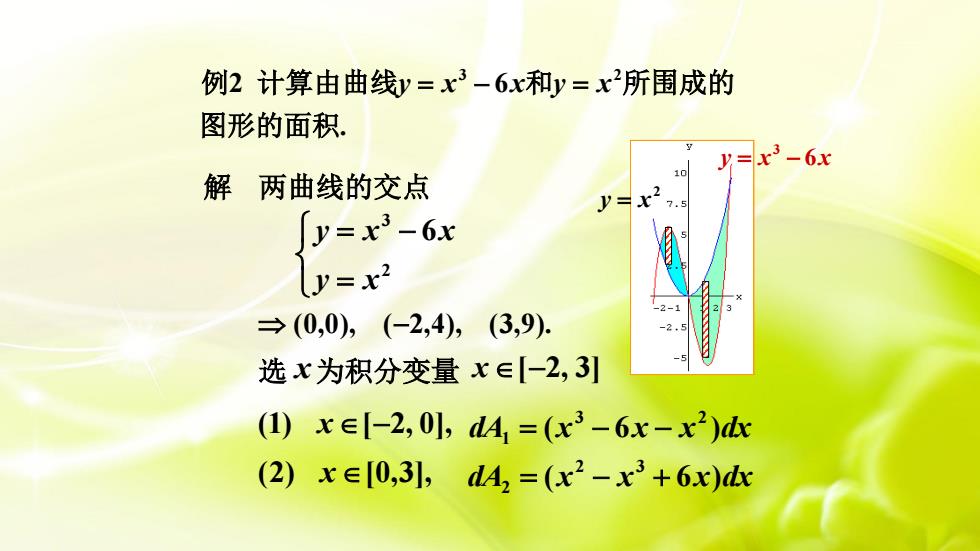
例2计算由曲线y=x3-6x和y=x2所围成的图形的面积y=x3 -6x10解两曲线的交点y=x2.[y= x3 -6x[y= x?-2-1→ (0,0), (-2,4),(3,9),选x为积分变量xE[-2,3](1) x[-2, 0], dA, =(x3 -6x -x')dx(2) xE[0,3], dA, =(x2 -x3 +6x)dx
解 两曲线的交点 (0,0), (−2,4), (3,9). = = − 2 3 6 y x y x x 选 x 为积分变量 x [−2, 3] (1) x [−2, 0], dA (x 6x x )dx 3 2 1 = − − (2) x [0,3], dA (x x 6x)dx 2 3 2 = − + 2 y = x y x 6x 3 = − 3 2 2 6 . 例 计算由曲线y x x y x = − = 和 所围成的 图形的面积