·48 第3章集合论 设A,4,,A是任意n个集合,则这n个集合的交可简记为凸A,即 I4=An4n∩An={z∈AZEAA A FEAn} E B (a)AnB≠a (b)AnB= 图3.4交运算的文氏图表示 交运算还可以推广到无穷多个集合的情况: A=A1∩42n∩4nn i=1 定义3.8设A、B是任意两个集合,由只属于A而不属于B的所有元素构成的集合 称为集合B对于A的相对补集(或A和B的差集),记作A-B. A-B={xx∈AAx年B} 例如,A={1,2,4,B={2,4,5},则A-B={1,B-A={5}. 集合B对于A的相对补运算的文氏图表示如图3.5(a)所示. (a)A-B (b)~A 图3.5补运算的文氏图表示 定义3.9设E为全集,A二E,则称集合A对于E的相对补集为A的绝对补集,记 作A. NA=E-A={xx∈EAx年A 例如,E={1,2,3,4,5},A={1,2,4,B={1,2,3,4,5},C=⑦,则~A={3,5} B=0~C=E. 集合A的绝对补运算的文氏图表示如图3.5(b)所示. 定义3.10设A、B是任意两个集合,由属于A但不属于B或者属于B但不属于A 的所有元素构成的集合称为集合A与B的对称差,记作A⊕B. A⊕B={x|(x∈AAx年B)V(x年AAx∈B)}
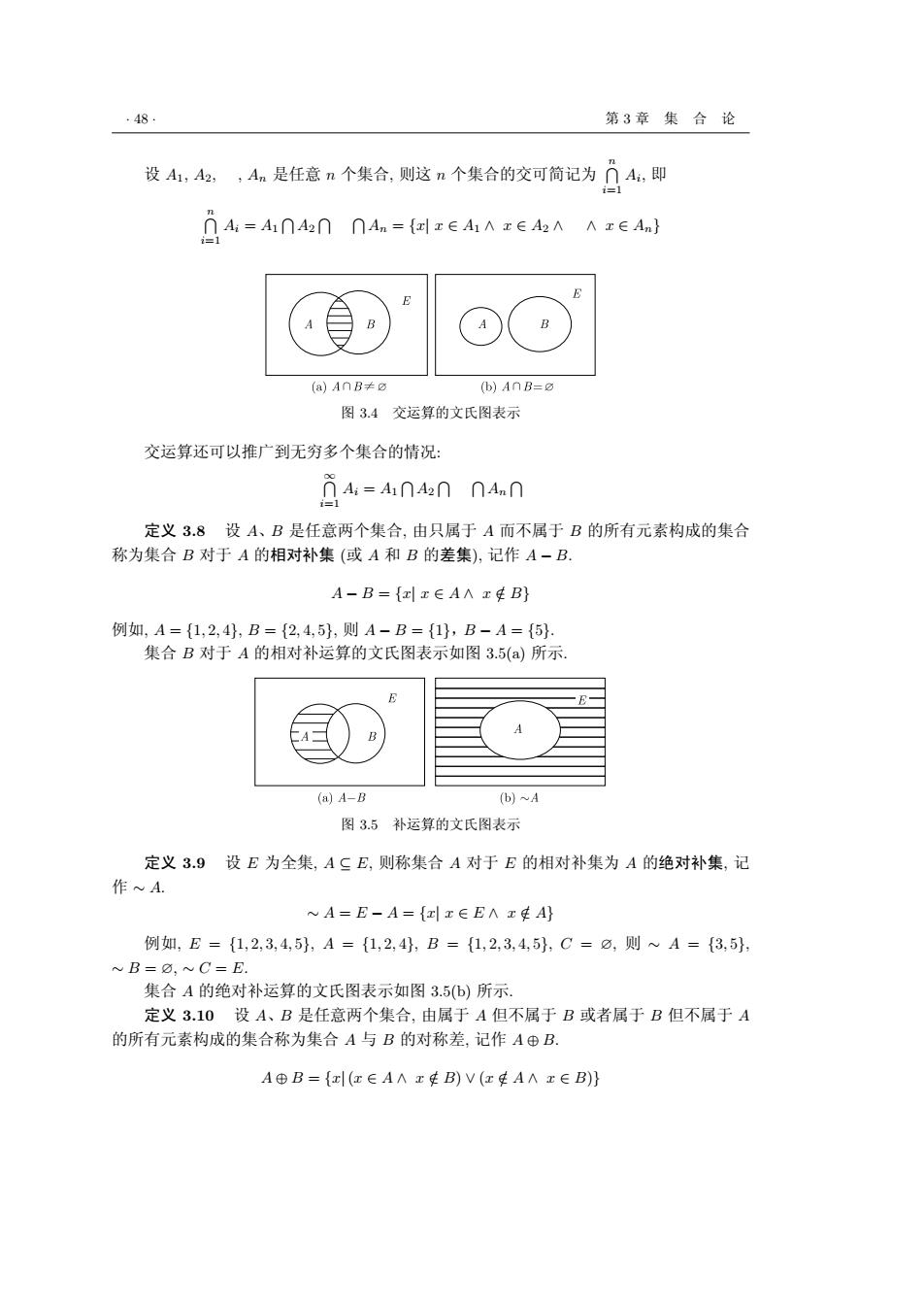
· 48 · 第 3 章 集 合 论 设 A1, A2, , An 是任意 n 个集合, 则这 n 个集合的交可简记为 Tn i=1 Ai , 即 Tn i=1 Ai = A1 T A2 T T An = {x| x ∈ A1 ∧ x ∈ A2 ∧ ∧ x ∈ An} 图 3.4 交运算的文氏图表示 交运算还可以推广到无穷多个集合的情况: T∞ i=1 Ai = A1 T A2 T T An T 定义 3.8 设 A、B 是任意两个集合, 由只属于 A 而不属于 B 的所有元素构成的集合 称为集合 B 对于 A 的相对补集 (或 A 和 B 的差集), 记作 A − B. A − B = {x| x ∈ A ∧ x /∈ B} 例如, A = {1, 2, 4}, B = {2, 4, 5}, 则 A − B = {1},B − A = {5}. 集合 B 对于 A 的相对补运算的文氏图表示如图 3.5(a) 所示. 图 3.5 补运算的文氏图表示 定义 3.9 设 E 为全集, A ⊆ E, 则称集合 A 对于 E 的相对补集为 A 的绝对补集, 记 作 ∼ A. ∼ A = E − A = {x| x ∈ E ∧ x /∈ A} 例如, E = {1, 2, 3, 4, 5}, A = {1, 2, 4}, B = {1, 2, 3, 4, 5}, C = ∅, 则 ∼ A = {3, 5}, ∼ B = ∅, ∼ C = E. 集合 A 的绝对补运算的文氏图表示如图 3.5(b) 所示. 定义 3.10 设 A、B 是任意两个集合, 由属于 A 但不属于 B 或者属于 B 但不属于 A 的所有元素构成的集合称为集合 A 与 B 的对称差, 记作 A ⊕ B. A ⊕ B = {x|(x ∈ A ∧ x /∈ B) ∨ (x /∈ A ∧ x ∈ B)}

3.3集合的运算 .49. 或 A⊕B=(A-B)八U(B-A) 集合A与B的对称差运算的文氏图表示如图3.6所示. 图3.6A⊕B的文氏图表示 例如,A={a,b,c,B={b,d,则A⊕B={a,c,d 从对称差的定义或文氏图容易看出 A⊕B=(AUB)-(A∩B) 该公式可作为A与B的对称差的一个等价定义. 设A、B、C为任意3个集合,对称差运算有以下性质: (1)A⊕B=B⊕A. (2)A⊕0=A. (3)A⊕A=0. (4)A⊕B=(A∩~B)U(~A∩B): (5)(A⊕B)⊕C=A⊕(B⊕C) (6)A∩(B⊕C)=(A∩B)⊕(A∩C) 3.3.2集合的运算律 集合运算同其他代数运算一样,都遵循一定的运算律.下面列出的是集合运算的主要运 算律,其中,E为全集,A、B、C为E的任意的3个子集 (1)幂等律 AUA=A,A∩A=A. (2)交换律 AUB=BUA,A∩B=B∩A (3)结合律 (AUB)UC=AU(BUC), (A∩B)∩C=A∩(B∩C) (4)分配律 AU(B∩C)=(AUB)∩(AUC), A∩(BUC)=(A∩B)U(A∩C). (⑤)吸收律 AU(A∩B)=A,A∩(AUB)=A (6)同一律 AU0=A,A∩E=A. (7)零律 AUE=E,A∩0=a. (8)排中律 AU~A=E. (⑨)矛盾律 A∩NA=0. (10)余补律 w⑦=E,E=⑦
3.3 集合的运算 · 49 · 或 A ⊕ B = (A − B) [ (B − A) 集合 A 与 B 的对称差运算的文氏图表示如图 3.6 所示. 图 3.6 A ⊕ B 的文氏图表示 例如, A = {a, b, c}, B = {b, d}, 则 A ⊕ B = {a, c, d}. 从对称差的定义或文氏图容易看出 A ⊕ B = (A S B) − (A T B) 该公式可作为 A 与 B 的对称差的一个等价定义. 设 A、B、C 为任意 3 个集合, 对称差运算有以下性质: (1) A ⊕ B = B ⊕ A. (2) A ⊕ ∅ = A. (3) A ⊕ A = ∅. (4) A ⊕ B = (A T ∼ B) S (∼ A T B). (5) (A ⊕ B) ⊕ C = A ⊕ (B ⊕ C). (6) A T (B ⊕ C) = (A T B) ⊕ (A T C). 3.3.2 集合的运算律 集合运算同其他代数运算一样, 都遵循一定的运算律. 下面列出的是集合运算的主要运 算律, 其中, E 为全集, A、B、C 为 E 的任意的 3 个子集. (1) 幂等律 A S A = A, A T A = A. (2) 交换律 A S B = B S A, A T B = B T A. (3) 结合律 (A S B) S C = A S (B S C), (A T B) T C = A T (B T C). (4) 分配律 A S (B T C) = (A S B) T (A S C), A T (B S C) = (A T B) S (A T C). (5) 吸收律 A S (A T B) = A, A T (A S B) = A. (6) 同一律 A S ∅ = A, A T E = A. (7) 零律 A S E = E, A T ∅ = ∅. (8) 排中律 A S ∼ A = E. (9) 矛盾律 A T ∼ A = ∅. (10) 余补律 ∼ ∅ = E, ∼ E = ∅