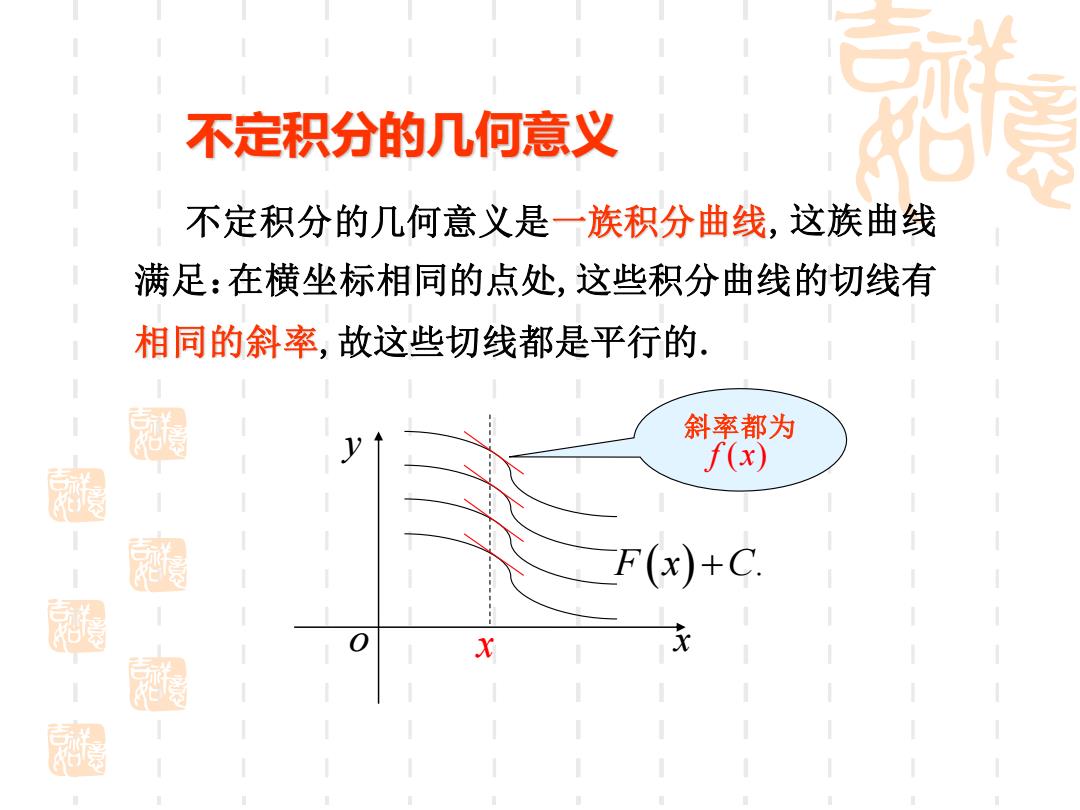
不定积分的几何意义 不定积分的几何意义是一族积分曲线,这族曲线 满足:在横坐标相同的点处,这些积分曲线的切线有 相同的斜率,故这些切线都是平行的, 斜率都为 f(x) 湿 F(x)+C. X
不定积分的几何意义 x y o F x C ( ) + . x 不定积分的几何意义是一族积分曲线, 在横坐标相同的点处,这些积分曲线的切线有 相同的斜率,故这些切线都是平行的. 斜率都为 f x( ) 这族曲线 满足:

3.1.2 基本积分公式 实例 --j +C.(4≠-1) 启示能否根据求导公式得出积分公式? 性质[f)了-[F()+c]=f) (2)∫F'(x)d=F(x)+C, 结论 微分运算与求不定积分的运算是互逆的
实例 x x = + + 1 1 . 1 1 C x x dx + + = + 启示 能否根据求导公式得出积分公式? ( −1) 3.1.2 基本积分公式 (1 ( ) ( ) ) f x dx F x C f x ( ) = + = (2 ( ) ( ) , ) F x dx F x C = + 结论 微分运算与求不定积分的运算是互逆的. 性质

(I)∫kd=c+C(k是常数); 基本积分公式 2∫x=+Cu*-: u+1 3)∫上k=lnl+c 说明:x>0,→∫ =Inx+C, x<0,m-∈女 →∫=la(-x)+C,÷∫=lnlx+C, 私极
基本积分公式 (1) kdx = kx + C (k 是常数); ( 1); 1 (2) 1 + − + = + C x x dx 1 (3) dx x 说明: x 0 , ln , = x + C x dx x 0, [ln( − x)] = , 1 ( ) 1 x x x − = − ln( ) , = − x + C x dx ln | | , = x + C x dx = ln x C+
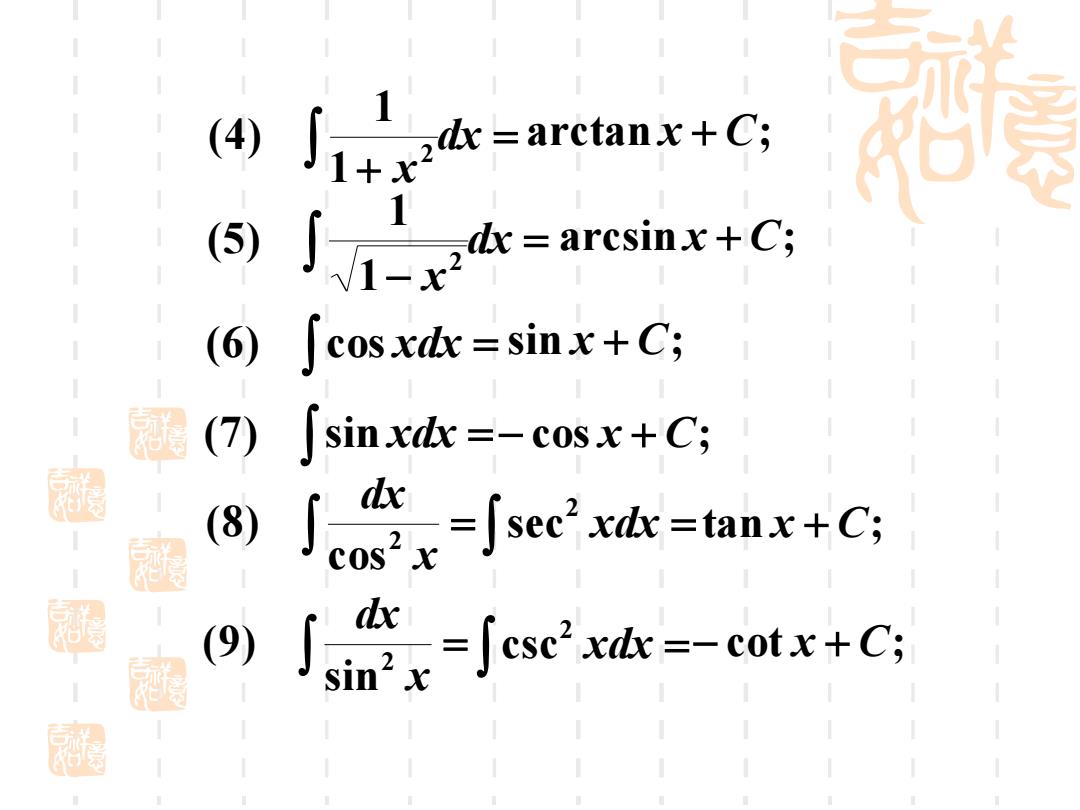
④j十血=aretan+C: ∫x=cin.+Cs (⑥)∫cosx=sinx+C; (7)∫sinxdx=-cosx+C; 涵 (8) jorv-jserh=tnx+c 涵 9) ∫-小es流=-eate+C
= + dx x 2 1 1 (4) arctan x + C; = − dx x 2 1 1 (5) arcsin x + C; (6) cos xdx = sin x + C; (7) sin xdx =− cos x + C; = x dx 2 cos (8) xdx = 2 sec tan x + C; = x dx 2 sin (9) xdx = 2 csc − cot x + C;

(10) ∫secxtanxdx=secx+C; (11)[cscxcotxdx=-cscx+C; (12)∫e*dk=e*+C; (13)∫rdk=0+C;a>,a味0 In a
(10) sec xtan xdx = sec x + C; (11) csc xcot xdx = − csc x + C; e dx = x (12) e C; x + a dx = x (13) ; ln C a a x + (a>0,a≠1)