
少例3求积分∫x2xd 解∫x2xd=∫x2d 1 限据积分公式2)x=牛 +C 5 +c-2x+c. +1 2
例3 求积分 . 2 x xdx 解 x xdx 2 x dx = 2 5 C x + + = + 1 2 5 1 2 5 . 7 2 2 7 = x + C 根据积分公式(2) C x x dx + + = + 1 1

3.1.3不定积分的运算性质 性质3-1[f(x)±g(xk=∫f(x)k±∫g(x)d, 证 [fx±∫g(x)k]' =[fx)]'±[s(x)]'=fe±gx 等式成立. (此性质可推广到有限多个函数之和的情况) 性质3-2∫f(x)akc=k∫f(x)ds (k是常数,k≠O)
[ ( ) ( )] f x g x dx = f x dx g x dx ( ) ( ) ; 证 f x dx g x dx ( ) ( ) f x dx g x dx ( ) ( ) = = f (x) g(x). 等式成立. (此性质可推广到有限多个函数之和的情况) kf x dx ( ) = k f x dx ( ) . (k是常数,k 0) 3.1.3 不定积分的运算性质 性质3-1 性质3-2
心例4求积分 3 dx 解 2 dx =可,e-1ec 涵 =3arctanx-2arcsinx+C 宝行骨8口
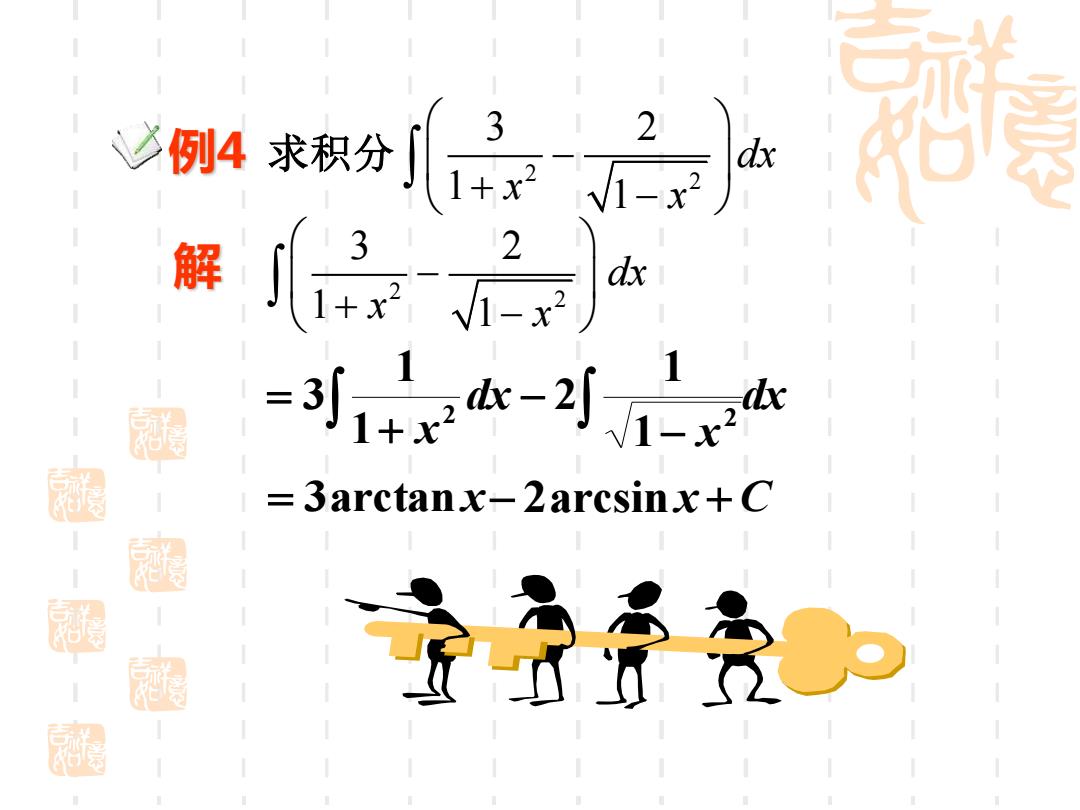
例4 求积分 解 2 2 3 2 1 1 dx x x − + − 2 2 3 2 1 1 dx x x − + − dx x dx x − − + = 2 2 1 1 2 1 1 3 = 3arctan x− 2arcsin x + C

之例5求积分 ∫(e-3cosx)a 解 ∫(e-3cosx =∫eak-3jcos,xdx =e*-3sin x+C 湖 少例6求积分「tan2xd 屦解∫tan2=∫(secx-i)dr tanx-x+C
例5 求积分 解 ( 3cos ) x e x dx − 3 cos x = − e dx xdx ( 3cos ) x e x dx − e x C x = − 3sin + 例6 求积分 xdx 2 tan 解 2 2 tan (sec 1) xdx x dx = − = − + tan x x C

必例7求积分 dx - 解 d dx 福 j-x+小+ -x+arctan+C 3
例7 求积分 解 4 2 1 x dx x + 2 2 2 ( 1)( 1) 1 1 x x dx x + − + = + 2 2 1 1 1 x dx x = − + + 2 2 1 1 x dx dx dx x = − + + x x C x = − + arctan + 3 3 4 2 1 x dx x +