第一节定积分的元素法 一、引例 二、元素法的步骤 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的元素法 一、引例 二、元素法的步骤
第一节定积分的元素法 一、 引例 引例曲边梯形的面积 在第五章第一节中,我们已经知道如图所示的曲边 梯形的面积可以用定积分来计算: A=fx)d y=f(x) 得到上述计算公式的步骤如下: 上页 下页 返回 MathGS 公式 线与面 数学家
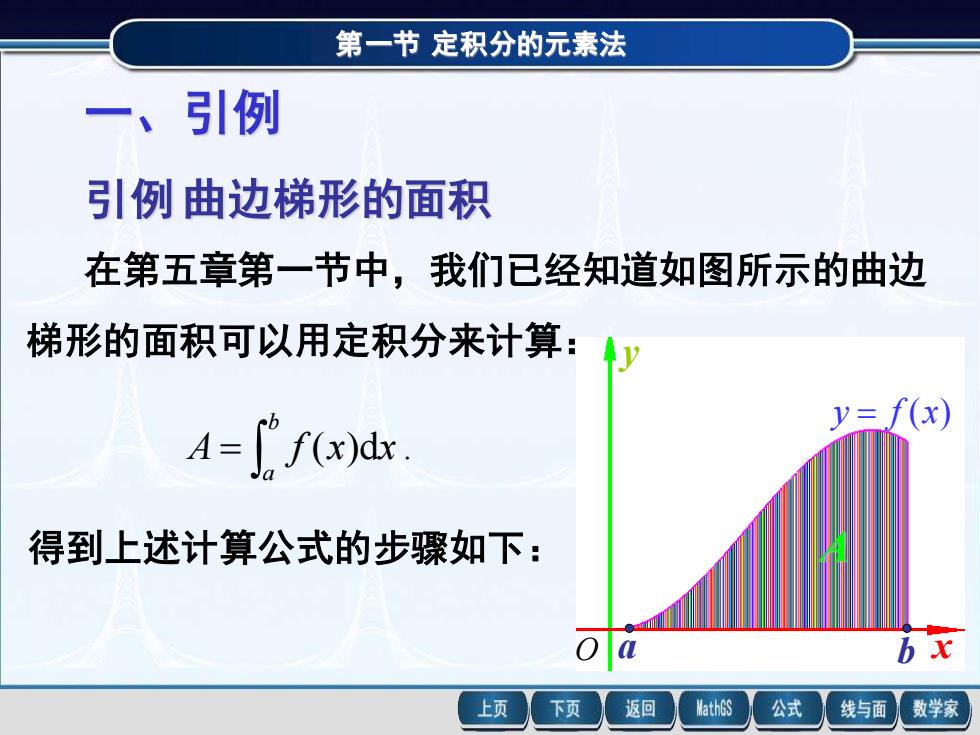
第一节 定积分的元素法 一、引例 引例 曲边梯形的面积 在第五章第一节中,我们已经知道如图所示的曲边 梯形的面积可以用定积分来计算: y = f (x) a b x y O A ( )d . = b a A f x x 得到上述计算公式的步骤如下:
第一节定积分的元素法 Step1分割把区间[a,bl任意分成n个小区间, 相应的大的曲边梯形也就分成了个小的曲边梯形, A=∑A4: i=1 y=f(x) Step2近似 △A,≈f(5)△x,(x-1≤5,≤x); Step3求和 A≈∑f5)Ax: i=1 Step4取极限 A=l1im∑f(5)△x=Cf(x)dx 1>0 i= 上页 下页 返回 MathGS 公式 线与面 数学家
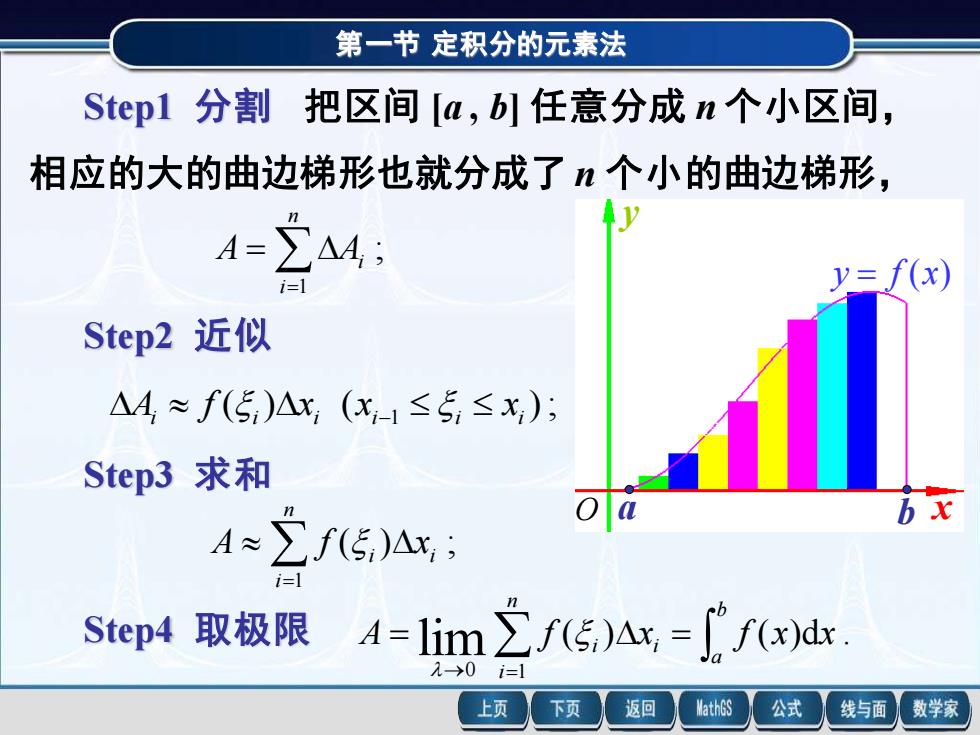
第一节 定积分的元素法 y = f (x) a b x y O Step1 分割 把区间 [a , b] 任意分成 n 个小区间, 相应的大的曲边梯形也就分成了 n 个小的曲边梯形, Step2 近似 ; 1 = = n i A Ai ( ) ( ); i i i i 1 i i A f x x x − Step3 求和 ( ) ; 1 = n i i i A f x Step4 取极限 ( ) ( )d . 0 1 lim = = → = b a n i i i A f x f x x

第一节定积分的元素法 在工程技术中,有很多量的计算,如旋转体的体积、 平行截面面积为已知的立体立体、曲线构件的长度、 变力沿直线所作的功、水压力、引力等,这些量的计 算都要用这种方法转化为定积分的计算.因此对这种方 法要进行研究和简化.研究和简化的结果就产生了元素 法 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的元素法 在工程技术中,有很多量的计算,如旋转体的体积、 平行截面面积为已知的立体立体、曲线构件的长度、 变力沿直线所作的功、 水压力、引力等,这些量的计 算都要用这种方法转化为定积分的计算. 因此对这种方 法要进行研究和简化. 研究和简化的结果就产生了元素 法

第一节定积分的元素法 二、元素法 设所求量为U,且U满足以下两个条件: (1)U与一个变量比如x的变化区间[a,b]有关; (2)对于区间[a,b]具有可加性:如果把区间[a,b] 分成许多部分区间,则U相应的分成许多部分量,而U 等于所有部分量的和。 那么U可用以下的元素法计算. 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的元素法 二、元素法 设所求量为 U ,且 U 满足以下两个条件: (1) U 与一个变量比如 x 的变化区间 [a , b ] 有关; (2) U 对于区间 [a , b ] 具有可加性:如果把区间[a , b] 分成许多部分区间,则 U 相应的分成许多部分量,而 U 等于所有部分量的和. 那么 U 可用以下的元素法计算