
第二节定积分在几何上的应用 一、平面图形的面积 二、体积 三、平面曲线的弧长 上页 下页 返回 MathS 公式 线与面 数学家
第二节 定积分在几何上的应用 一、平面图形的面积 二、体积 三、平面曲线的弧长
第二节定积分在几何上的应用 一、平面图形的面积 1.直角坐标情形 在直角坐标系下,积分变量一般 y=02(x) 取x或y.取x为积分变量时, 面积元素为小竖条,其面积可用如 图所示的小矩形近似: =0(x) dA=(x)-e(x)]dx,o a b 衣 故面积为 x+Ax A=[o,(x)-,(xdx 上页 下页 返回 MathGS 公式 线与面 数学家
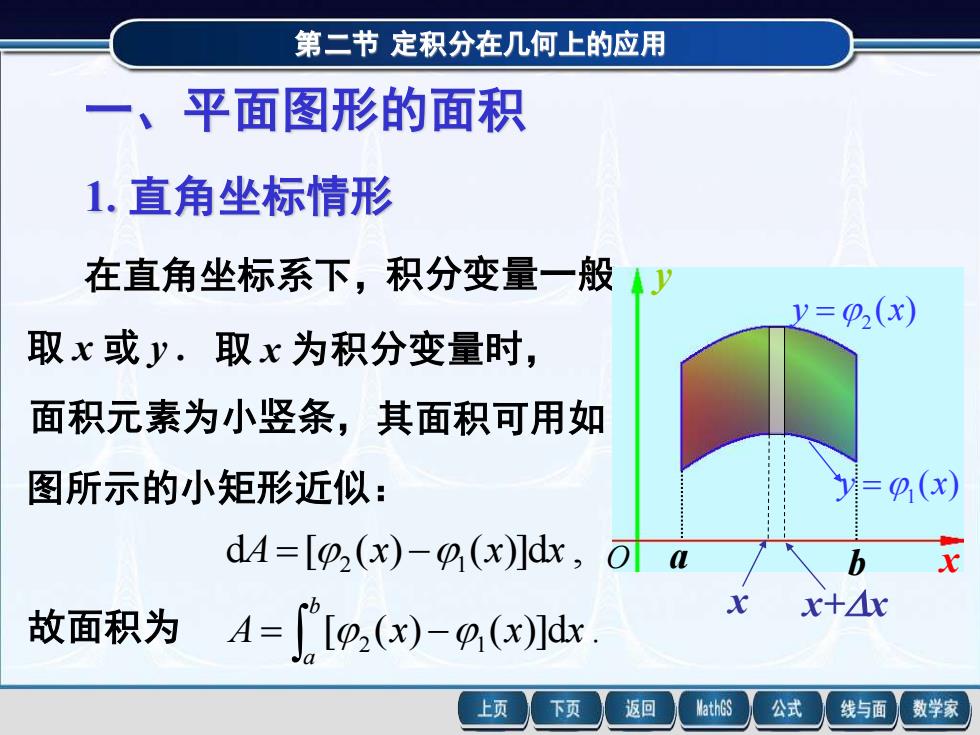
第二节 定积分在几何上的应用 一、平面图形的面积 1. 直角坐标情形 在直角坐标系下,积分变量一般 取 x 或 y . 取 x 为积分变量时, 面积元素为小竖条,其面积可用如 图所示的小矩形近似: d [ ( ) ( )]d , 2 1 A= x − x x 故面积为 [ ( ) ( )]d . = 2 − 1 b a A x x x x y O a b ( ) 1 y = x ( ) 2 y = x x x+x
第二节定积分在几何上的应用 取y为积分变量时,面积元素为小横条,其面积可 用如图所示的小矩形近似: d4=[W(y)-W(y)]dv, x=v(y)x=v2(y) d 故面积为 Jy+△y A=[[vz(y)-wi(y)]dy 上页 下页 返回 MathGS 公式 线与面 数学家
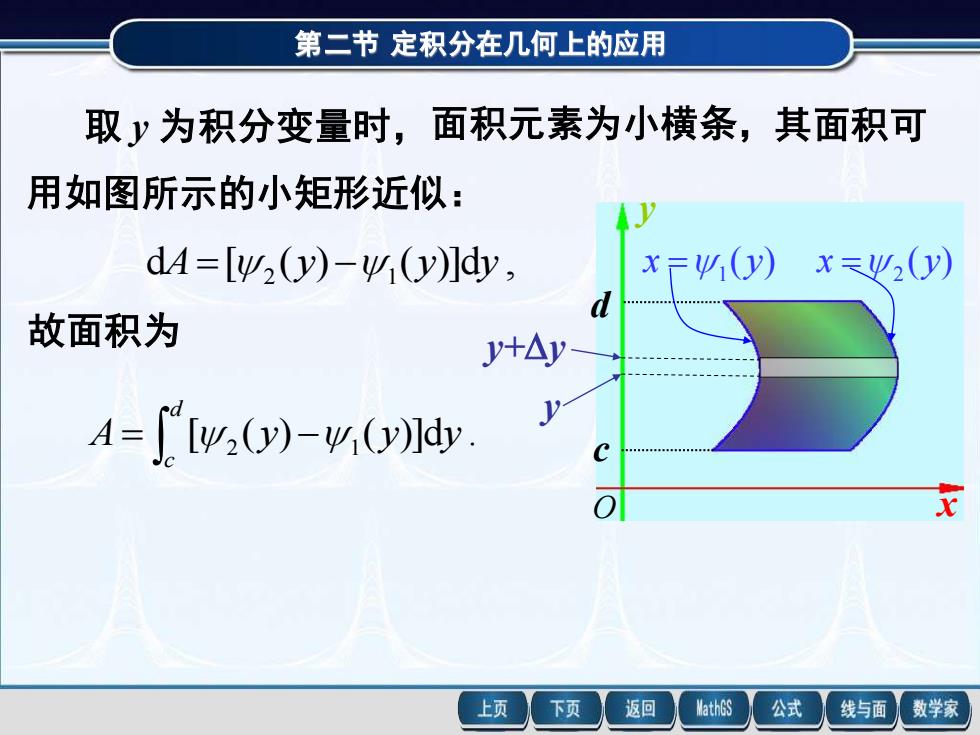
第二节 定积分在几何上的应用 取 y 为积分变量时,面积元素为小横条, 用如图所示的小矩形近似: d [ ( ) ( )]d , 2 1 A= y − y y 故面积为 [ ( ) ( )]d . = 2 − 1 d c A y y y 其面积可 O x y c d ( ) 1 x = y ( ) 2 x = y y y+y
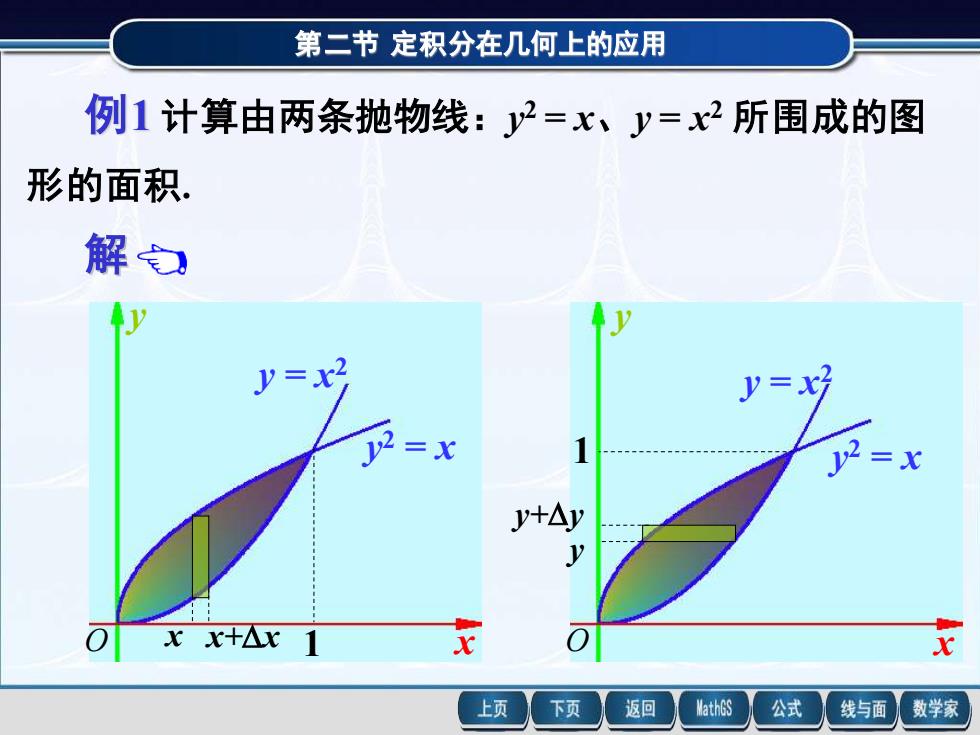
第二节定积分在几何上的应用 例1计算由两条抛物线:y2=x、y=x2所围成的图 形的面积. 解 y=x2 y+△y y xx+Ax 1 上页 下页 返回 MathGS 公式 线与面 数学家
第二节 定积分在几何上的应用 例1 计算由两条抛物线:y 2 = x、y = x 2 所围成的图 第二节 定积分在几何上的应用 解 例1 计算由两条抛物线:y 2 = x、y = x 2 所围成的图 形的面积. 先选 x 为积分变量,其 变化范围为 [0 , 1],此时微元为 小竖条,如图所示. 面积元素为 d ( )d . 2 A = x − x x 所求面积为 = − 1 0 2 A ( x x )dx 1 0 2 3 3 3 1 3 2 = x − x . 3 1 = y 2 = x y = x 2 x y O 1 x x+x 形的面积. y 2 = x y = x 2 x y O 1 x x+x y 2 = x y = x 2 x y O 1 y y+y
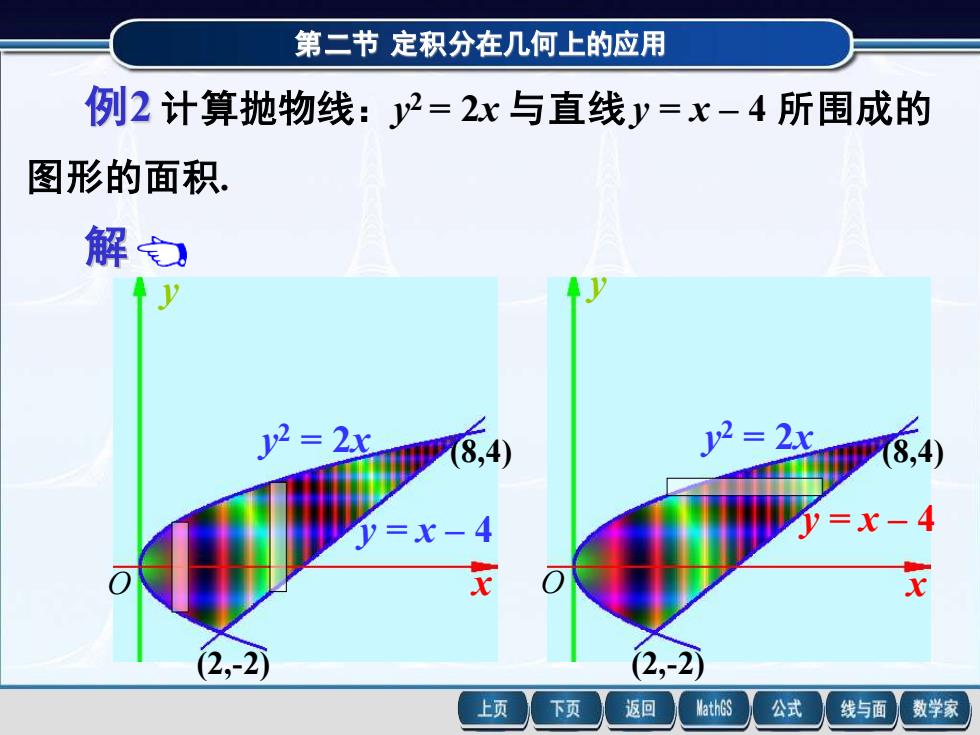
第二节定积分在几何上的应用 例2计算抛物线:y2=2x与直线y=x-4所围成的 图形的面积 解己 1 19 y2=2x Ψ8,4) y2=2x Ψ8,4) y=x-4 )=X-4 x x 2,-2 (2,-2 上页 下页 返回 MathGS 公式 线与面 数学家
第二节 定积分在几何上的应用 y 2 = 2x y = x – 4 x y O (2,-2) (8,4) 例2 计算抛物线:y 2 = 2x 与直线 y = x – 4 所围成的 第二节 定积分在几何上的应用 y 2 = 2x y = x – 4 x y O (2,-2) (8,4) 解 例2 计算抛物线:y 2 = 2x 与直线 y = x – 4 所围成的 图形的面积. 解方程组 = − = 4 2 2 y x y x 得抛物线和直线的交点为 (2 , -2) 和 (8 , 4) . 选 y 为积分变量,则面积元素为 d , 2 1 d 4 2 A y y y = + − 图形的面积. y 2 = 2x y = x – 4 x y O (2,-2) (8,4)