
第四节反常积分 一、无穷限的反常积分 二、无界函数的反常积分 上顷下页返回的公式线与通数学家
第四节 反常积分 一、无穷限的反常积分 二、无界函数的反常积分

第四节反常积分 一、无穷限的反常积分 1.定义 定义1设函数fx)在区间[a,+oo)上连续,取t>, 如果极限1if(x)d存在,则称此极限为函数fw) 在无穷区间[a,+o)上的反常积分,记作f(x)dx,即 f(d-lim[fd t+00 此时也称反常积分收敛,如果极限不存在,则称发散 上页 下页 返回 MathGS 公式 线与面 数学家
第四节 反常积分 一、无穷限的反常积分 定义1 设函数 f (x) 在区间 [a , +) 上连续,取 t > a, 如果极限 →+ t a t f (x)dx lim 存在, 在无穷区间 [a , +) 上的反常积分,记作 ( )d , + a f x x 即 ( )d ( )d . lim →+ + = t a t a f x x f x x 此时也称反常积分收敛,如果极限不存在,则称发散. 则称此极限为函数 f (x) 1. 定义

第四节反常积分 类似地可定义: f()dx=limf(d [f()dx=f()dx+[f(x)dx limfdx+limf()d 上页 下页 返回 MathGS 公式 线与面 数学家
第四节 反常积分 类似地可定义: ( )d ( )d . lim →− − = b t t b f x x f x x ( )d ( )d . ( )d ( )d ( )d 0 0 0 0 lim lim →− →+ + − + − = + = + t t t t f x x f x x f x x f x x f x x

第四节反常积分 2.计算方法 设Fx)为fx)在区间[a,+o)上的一个原函数,若 limF(x)存在,则有计算公式 x→+00 f(x)dx=lim F(x)-F(@)=[F(x X→十00 f(x)dx=F(b)-lim F(x)=[F() f(x)dx=lim F(x)-lim F(x)=[F(x X)+0∞ X→-00 上页 下页 返回 MathGS 公式 线与面 数学家
第四节 反常积分 2. 计算方法 设 F(x) 为 f (x) 在区间 [a , +) 上的一个原函数,若 ( ) limF x x→+ 存在,则有计算公式 ( )d ( ) ( ) [ ( )] . lim + →+ + = − = a x a f x x F x F a F x ( )d ( ) ( ) [ ( )] . lim b x b f x x F b F x F x − →− − = − = ( )d ( ) ( ) [ ( )] . lim lim + − →+ →− + − = − = f x x F x F x F x x x
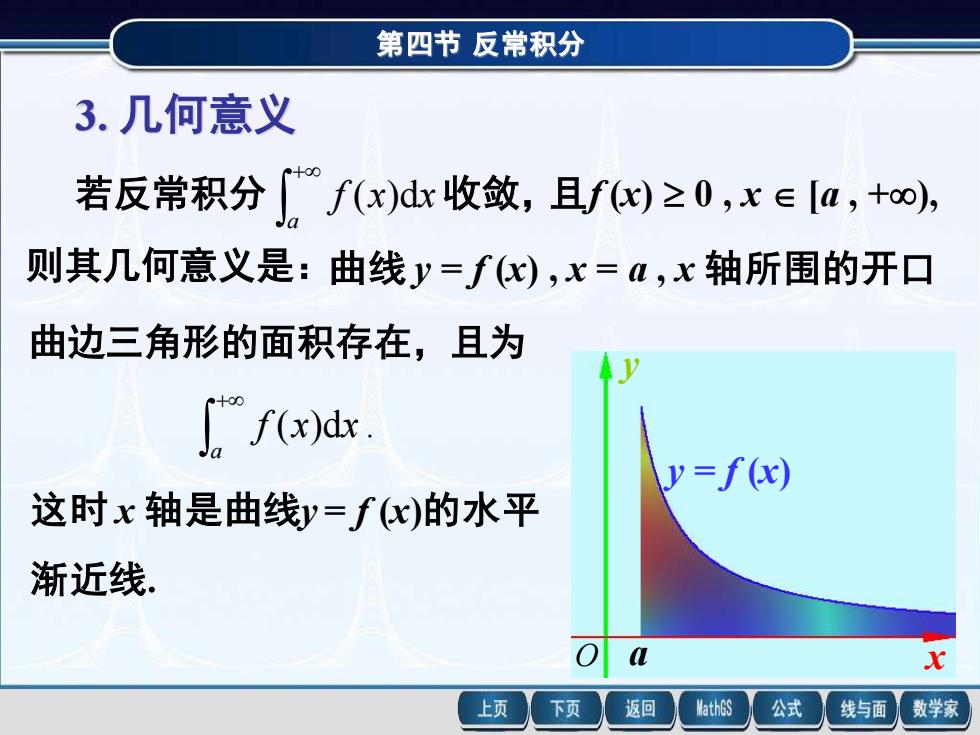
第四节反常积分 3.几何意义 若反常积分f(x)dx收敛,且fe)≥0,x∈[a,+o), 则其几何意义是:曲线y=fx),x=a,x轴所围的开口 曲边三角形的面积存在,且为 ["fodas y=f(x) 这时x轴是曲线y=fx)的水平 渐近线. 上页 下页 返回 MathGS 公式 线与面 数学家
第四节 反常积分 3. 几何意义 若反常积分 + a f (x)dx 收敛, 则其几何意义是: 曲边三角形的面积存在,且为 ( )d . + a f x x 这时 x 轴是曲线y = f (x)的水平 渐近线. 且f (x) 0 , x [a , +), 曲线 y = f (x) , x = a , x 轴所围的开口 a x y y = f (x) O