
第一节定积分的概念与性质 一、定积分问题举例 二、定积分定义 三、定积分的近似计算 四、定积分的性质 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 一、定积分问题举例 二、定积分定义 三、定积分的近似计算 四、定积分的性质
第一节定积分的概念与性质 一、定积分问题举例 1.曲边梯形的面积 我们已经会求规则平面图形的面积,如 矩形 平行四边形 三角形 梯形 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 一、定积分问题举例 1. 曲边梯形的面积 我们已经会求规则平面图形的面积,如 矩形 平行四边形 三角形 梯形

第一节定积分的概念与性质 那么如何求不规则平面图形的面积呢?如 y =1.5xsin x -2L 2 X 下面来研究这个问题. 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 那么如何求不规则平面图形的面积呢?如 下面来研究这个问题. x y y =1.5xsin x -2 2 O
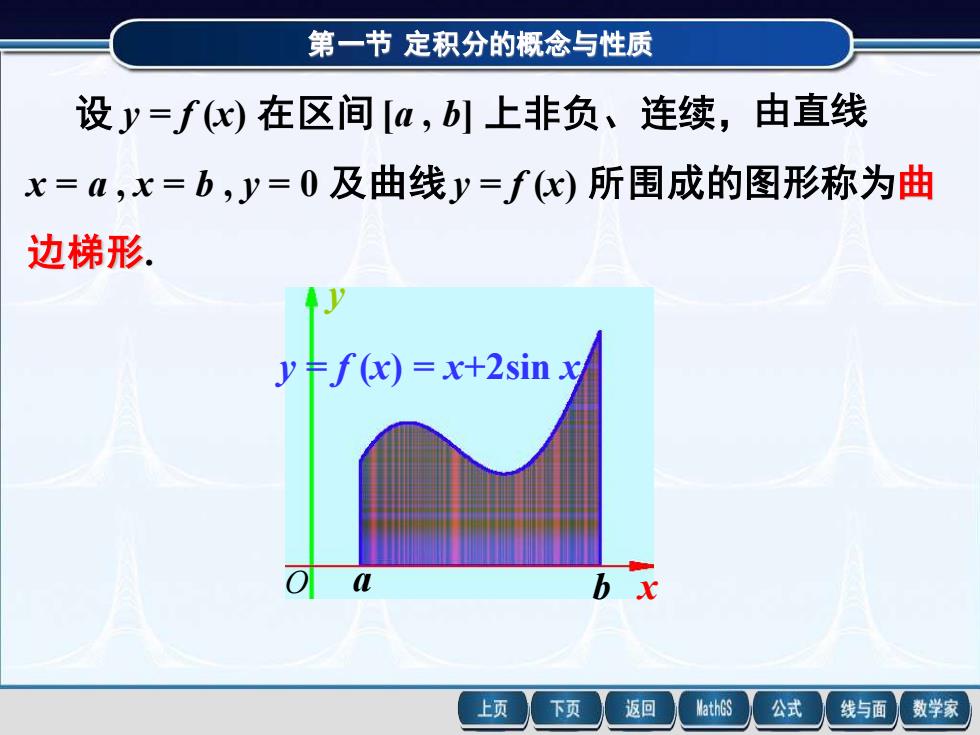
第一节定积分的概念与性质 设y=f心)在区间[a,b1上非负、连续,由直线 x=,x=b,y=0及曲线y=f(x)所围成的图形称为曲 边梯形 y卡f(x)=x+2sinx 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 设 y = f (x) 在区间 [a , b] 上非负、连续,由直线 x = a , x = b , y = 0 及曲线 y = f (x) 所围成的图形称为曲 边梯形. x y a b y = f (x) = x+2sin x O
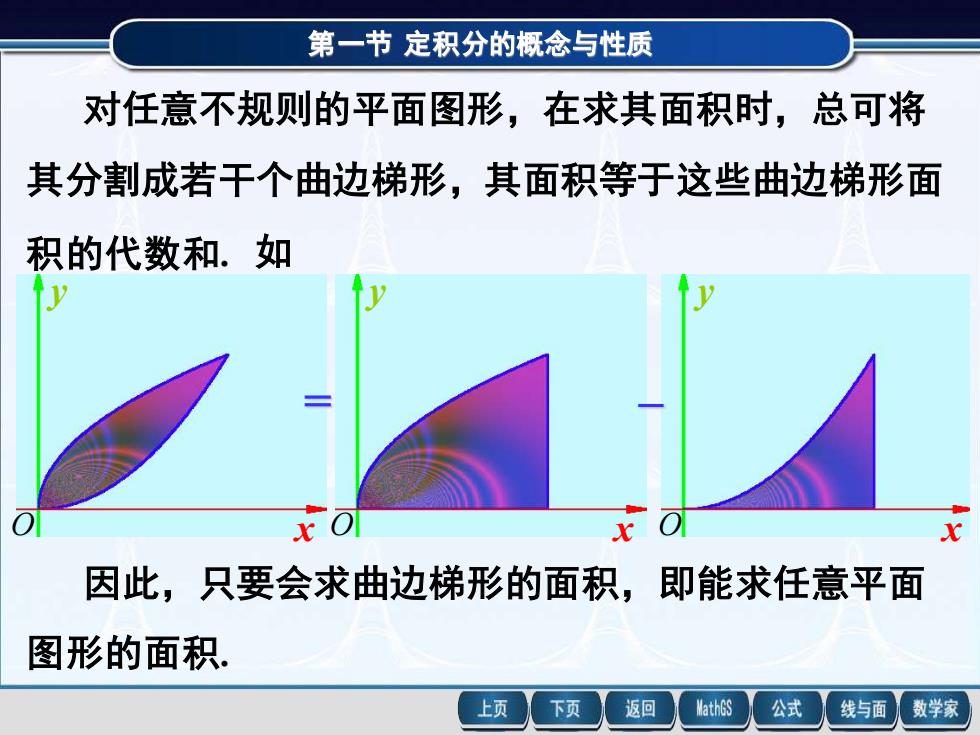
第一节定积分的概念与性质 对任意不规则的平面图形,在求其面积时,总可将 其分割成若干个曲边梯形,其面积等于这些曲边梯形面 积的代数和.如 1 因此,只要会求曲边梯形的面积,即能求任意平面 图形的面积. 上页 下页 返回 MathGS 公式 线与面 数学家
第一节 定积分的概念与性质 O x y O x y O x y 对任意不规则的平面图形,在求其面积时,总可将 其分割成若干个曲边梯形,其面积等于这些曲边梯形面 积的代数和. 如 = – 因此,只要会求曲边梯形的面积,即能求任意平面 图形的面积