
第三节定积分的换元法和分部积分法 一、定积分的换元法 二、定积分的分部积分法 上页下页 返回Math6公式 线与面数学家
第三节 定积分的换元法和分部积分法 一、定积分的换元法 二、定积分的分部积分法

第三节定积分的换元法和分部积分法 一、定积分的换元法 定理假设函数fw)在区间[a,)上连续,函数 x=p)满足条件: (1)p(叫=a,(=b; 2)p)在[a,上具有连续导数,且其值域R。= [a,b], 则有 f(x)x=(dr 换元公式 证明 上页 下页 返回 MathGS 公式 线与面 数学家
第三节 定积分的换元法和分部积分法 一、定积分的换元法 定理 假设函数 f (x) 在区间 [a , b] 上连续,函数 x = (t) 满足条件: (1) () = a , () = b ; (2) (t) 在 [ , ] 上具有连续导数,且其值域 R = [a , b], 则有 ( )d [ ( )] ( )d . = f x x f t t t b a 换元公式 第三节 定积分的换元法和分部积分法 证明 (1) () = a , () = b ; (2) (t) 在 [ , ] 上具有连续导数,且其值域 R = [a , b], 假设 F(x) 是 f (x) 的一个原函数,则 f (x)dx F(b) F(a). b a = − 另一方面,记 (t) = F[(t)],则 Φ(t) = f [(t)](t) , 于是 [( )] ( )d ( ) () f t t t = Φ −Φ = F[()]− F[()] = F(b) − F(a) ( )d . = b a f x x 证毕

第三节定积分的换元法和分部积分法 几点说明: (1)用x=p()换元时,积分限也要换成新变量的积 分限(换元必换限); (2)求出f[p'的一个原函数后,不需代回 原来的变量,直接计算(-()即可. 3)换元公式相当于不定积分的第二换元积分法,反 过来用换元公式即为凑微分法,用凑微分法能直接算出 原函数时,可以不换元 上页 下页 返回 MathGS 公式 线与面 数学家
第三节 定积分的换元法和分部积分法 几点说明: (1) 用 x = (t) 换元时,积分限也要换成新变量的积 分限(换元必换限); (2) 求出 f [(t)] (t) 的一个原函数(t) 后,不需代回 原来的变量,直接计算() - () 即可. (3) 换元公式相当于不定积分的第二换元积分法,反 过来用换元公式即为凑微分法,用凑微分法能直接算出 原函数时,可以不换元
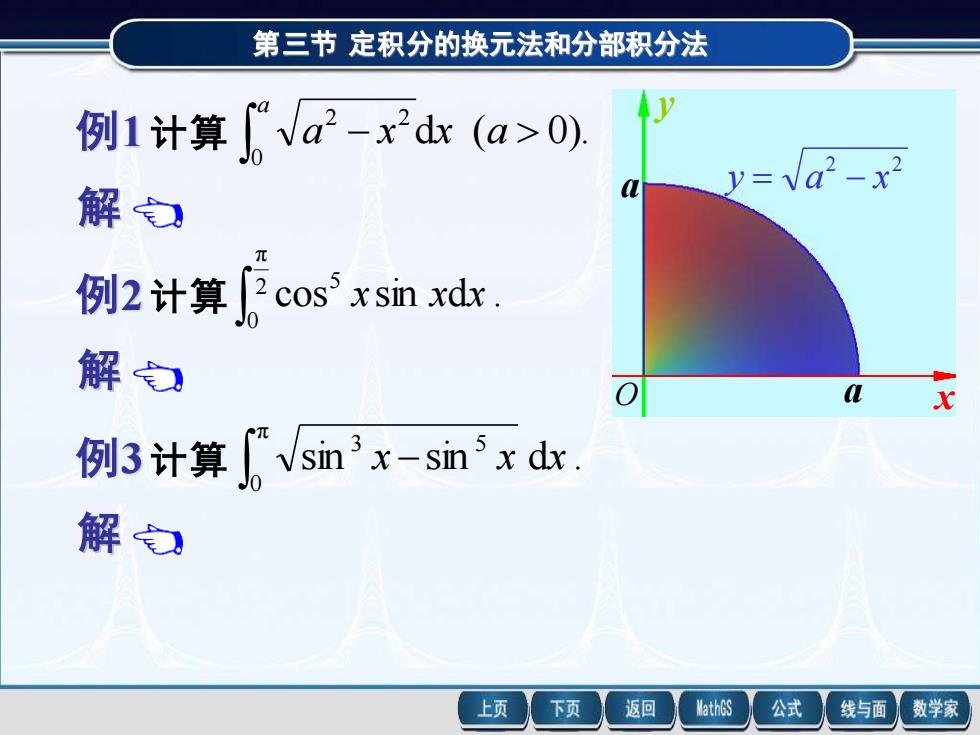
第三节定积分的换元法和分部积分法 例1计算心Va2-x2d(a>0) y=Va2-x2 解 例2计算2 cosxsin xdx 解 X 例3计算vsin3x-sn5xdk 解 上页 下页 返回 MathGS 公式 线与面 数学家
第三节 定积分的换元法和分部积分法 例1 计算 d ( 0). 0 2 2 − a x x a a 第三节 定积分的换元法和分部积分法 解 例1 计算 d ( 0). 0 2 2 − a x x a a 令 x = a sin t,则 dx = a cos t dt, 当 x = 0 时,取 t = 0; 当 x = a 时,取 t = /2 . 于是 − a a x x 0 2 2 d = 2 π 0 2 2 a cos t dt = + 2 π 0 2 (1 cos 2 ) d 2 t t a 2 π 0 2 sin 2 2 1 2 = t + t a . 4 π 2 a = 例2 计算 cos sin d . 2 π 0 5 x x x 第三节 定积分的换元法和分部积分法 解 例2 计算 cos sin d . 2 π 0 5 x x x 2 π 0 5 cos xsin xdx = 2 π 0 5 cos xd cos x 不作变量代换 2 π 0 cos 6 1 = x . 6 1 = 作变量代换 令 t = cos x , 则 dt = -sin x dx , 且 当 x = 0 时,t = 1; 当 x = /2 时,t = 0 . 于是 2 π 0 5 cos xsin xdx = − 0 1 5 t dt = 1 0 5 t dt . 6 1 = 例3 计算 sin sin d . π 0 3 5 x − x x 第三节 定积分的换元法和分部积分法 解 例3 计算 sin sin d . π 0 3 5 x − x x 由于 x x 3 5 sin −sin sin | cos | , 2 3 = x x − π 0 3 5 sin x sin x dx = + π 2 π 2 3 2 π 0 2 3 sin x | cos x | dx sin x | cos x | dx = − π 2 π 2 3 2 π 0 2 3 sin x cos x dx sin x cos x dx 所以 π 2 π 2 5 2 π 0 2 5 sin 5 2 sin 5 2 − = x x . 5 4 = a a 2 2 y = a − x x y O

第三节定积分的换元法和分部积分法 例4计算 X+2 dx 解 例5证明: ()若fx)在【-,上连续且为偶函数,则 f(x)dx=2f(x)dx. (2)若fx)在【-M,上连续且为奇函数,则 巴faw)dr=0 证明 上页 下页 返回 MathGS 公式 线与面 数学家
第三节 定积分的换元法和分部积分法 例4 计算 d . 2 1 4 2 0 + + x x x 第三节 定积分的换元法和分部积分法 解 例4 计算 d . 2 1 4 2 0 + + x x x 设 2x +1 = t , 则 , d d , 2 1 2 x t t t x = − = 且 当 x = 0 时,t = 1 ; 当 x = 4 时,t = 3 . 于是 + 4 + 0 d 2 1 2 x x x + − = 3 1 2 d 2 2 1 t t t t = + 3 1 2 ( 3) d 2 1 t t 3 1 3 3 2 3 1 = + t t . 3 22 = 例5 证明: ( ) d 2 ( ) d . 0 = − a a a f x x f x x 第三节 定积分的换元法和分部积分法 证明 ( ) d 2 ( ) d . 0 = − a a a f x x f x x ( ) d = 0 . − a a f x x 当 f(x) 为偶函数时 当 f(x) 为奇函数时 因为 ( ) d ( ) d ( ) d , 0 0 = + − − a a a a f x x f x x f x x 对积分 − 0 ( ) d a f x x 作变量代换 x = - t,则得 − 0 ( ) d a f x x = − − 0 ( ) d a f t t ( ) d . 0 = − a f x x 所以 ( ) d [ ( ) ( )] d . 0 = + − − a a a f x x f x f x x (1) 若 f (x) 在 [-a , a] 上连续且为偶函数,则 ( ) d = 0 . − a a f x x (2) 若 f (x) 在 [-a , a] 上连续且为奇函数,则