
习题课 第六章 定积分的左用 1.定积分的应用 几何方面:面积、体积、弧长、表面积 物理方面:质量、作功、侧压力、引力、 转动惯量 2.基本方法:微元分析法 微元形状:条、段、带、片、扇、环、壳等 HIGH EDUCATION PRESS 机动目录上页下页返回结束
习题课 1. 定积分的应用 几何方面 : 面积、体积、弧长、表面积 . 物理方面 : 质量、作功、侧压力、引力、 2. 基本方法 : 微元分析法 微元形状 : 条、段、带、片、扇、环、壳 等. 转动惯量 . 机动 目录 上页 下页 返回 结束 定积分的应用 第六章
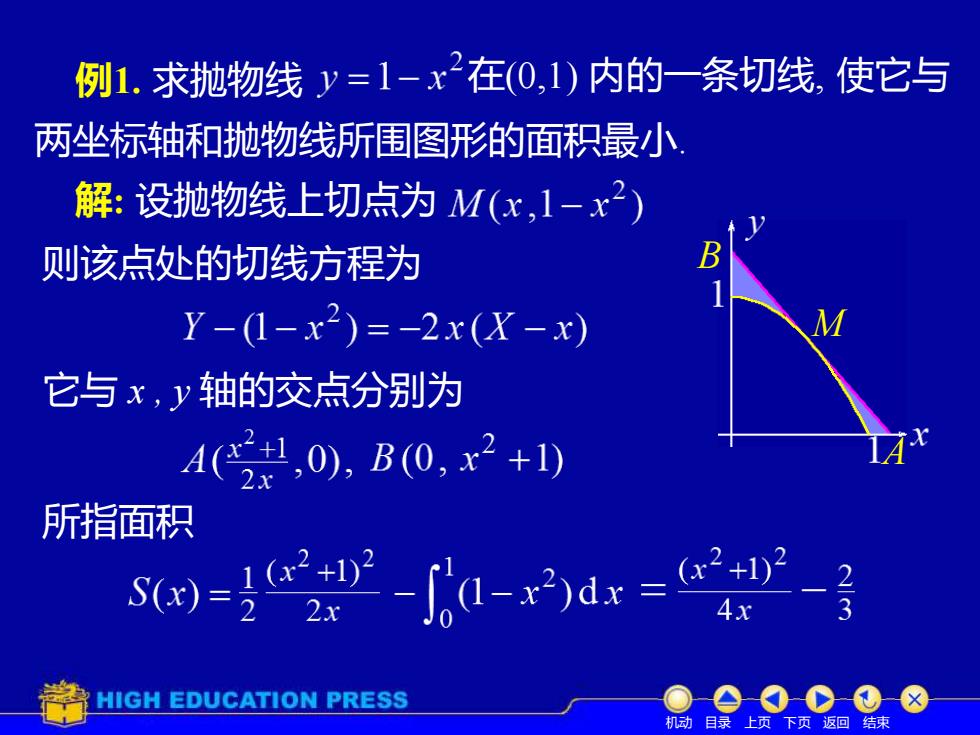
例1.求抛物线y=1-x在(0,1)内的一条切线,使它与 两坐标轴和抛物线所围图形的面积最小 解:设抛物线上切点为M(x,1-x2) 则该点处的切线方程为 Y-1-x2)=-2x(X-x) 它与x,y轴的交点分别为 1(2,0),B(0,x2+1) 所指面积 s=-a-dx=- HIGH EDUCATION PRESS 机动目 页返回结束
例1. 求抛物线 在(0,1) 内的一条切线, 使它与 两坐标轴和抛物线所围图形的面积最小. 解: 设抛物线上切点为 则该点处的切线方程为 它与 x , y 轴的交点分别为 所指面积 M B A 机动 目录 上页 下页 返回 结束

S()=x2+)6x2-1) 令S(x)=0,得0,1]上的唯一驻点x= x<晋,S()<0 x>等,S()>0 因此x=5是S(x)在[0,]上的唯一极小点, 且为最小点.故所求切线为 23 4 X+ HIGH EDUCATION PRESS DeOC①8 机动目录上页下页返回结束
且为最小点 . 故所求切线为 得[ 0 , 1] 上的唯一驻点 M B A 机动 目录 上页 下页 返回 结束

例2.设非负函数f(x)在[0,1]上满足xf'(x)=f(x) +9x2,曲线y=∫()与直线x=1及坐标轴所围图形 面积为2, (1)求函数f(x): (2)α为何值时,所围图形绕x轴一周所得旋转体 体积最小? 解:(1)当x≠0时,由方程得 xf(x)-f(x)3 2 即r/1-a 故得 3 f(x)=。ax2+Cx HIGH EDUCATION PRESS 机动目录上页下页返回结束
例2. 设非负函数 曲线 与直线 及坐标轴所围图形 (1) 求函数 (2) a 为何值时, 所围图形绕 x 轴一周所得旋转体 解: (1) 由方程得 面积为 2 , 体积最小 ? 即 故得 机动 目录 上页 下页 返回 结束

又 2-/d=-a2+c)s-+9 C4-af-ar2+4-a (2)旋转体体积 -e产ao 令r=(5a+1)=0,得a=5 又 V"la=-5- .a=-5为唯一极小点,因此a=-5时V取最小值 HIGH EDUCATION PRESS ●◆00⊙8 机动目录上页下页返回结束
又 (2) 旋转体体积 又 为唯一极小点, 因此 时 V 取最小值 . x o y 1 x o y 1 机动 目录 上页 下页 返回 结束